Tìm GTLN ( hoặc GTNN ) của biểu thức sau :
\(D=\dfrac{x^2}{x-2}.\left(\dfrac{x^2+4}{x}-4\right)+3\)
PP
Những câu hỏi liên quan
ND
23 tháng 5 2023 lúc 22:14
Tìm GTNN và GTLN nếu có của các biểu thức
\(A=\dfrac{2x^2-2x+5}{\left(x+1\right)^2}\)
\(B=\dfrac{4x^2+x+4}{x^2+x+1}\)
Biểu thức nào em?
Đúng 0
Bình luận (1)
Tìm GTLN và GTNN nếu có của các biểu thức sau :
a. \((x+\dfrac{2}{3})^2+\dfrac{1}{2}với(x\in Q)\)
b.\(\left|x-2020\right|+2021\)
Bài 4: Cho biểu thức A \(=\left(\dfrac{1}{x+2}-\dfrac{2}{x-2}-\dfrac{x}{4-x^2}\right):\dfrac{6\left(x+2\right)}{\left(2-x\right)\left(x+1\right)}\)
a) Rút gọn A
b)Tìm x để A > 0
c) Tìm x biết x2 + 3x + 2 \(=0\)
d) Tìm x để A đạt GTLN, tìm GTLN đó
a: \(A=\dfrac{x-2-2x-4+x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-\left(x-2\right)\left(x+1\right)}{6\left(x+2\right)}\)
\(=\dfrac{-6}{\left(x+2\right)}\cdot\dfrac{-\left(x+1\right)}{6\left(x+2\right)}=\dfrac{\left(x+1\right)}{\left(x+2\right)^2}\)
b: A>0
=>x+1>0
=>x>-1
c: x^2+3x+2=0
=>(x+1)(x+2)=0
=>x=-2(loại) hoặc x=-1(loại)
Do đó: Khi x^2+3x+2=0 thì A ko có giá trị
Đúng 0
Bình luận (0)
Tìm GTLN hoặc GTNN (nếu có) của A dfrac{-4x^2}{-left(x-3right)^2}
Giải phuong trình sau: 8left(x+dfrac{1}{x}right)^2+4left(x^2+dfrac{1}{x^2}right)^2-4left(x^2+dfrac{1}{x^2}right).left(x+dfrac{1}{x}right)^2left(x+4right)^2
Tìm GTNN của biêu thức: Ax^2-2xy+2y^2+6x-14y+25
Giải phương trình: x^4+8x^3+14x^2-8x+10
Đọc tiếp
Tìm GTLN hoặc GTNN (nếu có) của A= \(\dfrac{-4x^2}{-\left(x-3\right)^2}\)\
Giải phuong trình sau: \(8\left(x+\dfrac{1}{x}\right)^2+4\left(x^2+\dfrac{1}{x^2}\right)^2-4\left(x^2+\dfrac{1}{x^2}\right).\left(x+\dfrac{1}{x}\right)^2=\left(x+4\right)^2\)
Tìm GTNN của biêu thức: \(A=x^2-2xy+2y^2+6x-14y+25\)
Giải phương trình: \(x^4+8x^3+14x^2-8x+1=0\)
1. Tìm GTNN của \(y=x+\dfrac{1}{x}-5\) trên \(\left(0,+\infty\right)\)
2. Tìm GTNN của \(y=4x^2+\dfrac{1}{x}-4\) trên \(\left(0,+\infty\right)\)
3. Tìm GTLN của \(y=\dfrac{x^2+4}{x}\) trên \(\left(-\infty,0\right)\)
\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)
\(y_{min}=-3\) khi \(x=1\)
\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)
\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)
\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)
\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)
Đúng 0
Bình luận (0)
B1:Cho biểu thức Aleft(dfrac{1}{x+2}-dfrac{2}{x-2}-dfrac{x}{4-x}right):dfrac{6left(x+2right)}{left(2-xright)left(x+1right)}a. Rút gọn biểu thức Ab. Tìm x để A 0c. Tìm x biết x^2+3x+20 d. Tìm x để A đạt GTLN, tìm GTLN đó.Cho biểu thứcAleft(dfrac{2+x}{2-x}-dfrac{2-x}{2+x}-dfrac{4x^2}{x^2-4}right):dfrac{x^2-6x+9}{left(2-xright)left(x-3right)} a. Rút gọn Ab. Tính giá trị của A biết left|x-5right|2 c. Tìm giá trị nguyên dương của x để A 4 và A có giá trị là một số...
Đọc tiếp
B1:Cho biểu thức \(A=\left(\dfrac{1}{x+2}-\dfrac{2}{x-2}-\dfrac{x}{4-x}\right):\dfrac{6\left(x+2\right)}{\left(2-x\right)\left(x+1\right)}\)
a. Rút gọn biểu thức A
b. Tìm x để A > 0
c. Tìm x biết \(x^2+3x+2=0\)
d. Tìm x để A đạt GTLN, tìm GTLN đó.
Cho biểu thức\(A=\left(\dfrac{2+x}{2-x}-\dfrac{2-x}{2+x}-\dfrac{4x^2}{x^2-4}\right):\dfrac{x^2-6x+9}{\left(2-x\right)\left(x-3\right)}\)
a. Rút gọn A
b. Tính giá trị của A biết \(\left|x-5\right|=2\)
c. Tìm giá trị nguyên dương của x để A < 4 và A có giá trị là một số nguyên.
B1: ĐXXĐ: \(x\ne\pm2;x\ne-1\)
\(=\left(\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}-\dfrac{2\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}+\dfrac{x}{\left(x+2\right)\left(x-2\right)}\right):\dfrac{-6\left(x+2\right)}{\left(x-2\right)\left(x+1\right)}\)
\(=\left(\dfrac{x-2-2x-2+x}{\left(x+2\right)\left(x-2\right)}\right):\dfrac{-6\left(x+2\right)}{\left(x-2\right)\left(x+1\right)}\)
\(=\dfrac{-4}{\left(x+2\right)\left(x-2\right)}:\dfrac{-6\left(x+2\right)}{\left(x-2\right)\left(x+1\right)}\)
\(=\dfrac{-4}{\left(x+2\right)\left(x-2\right)}.\dfrac{\left(x-2\right)\left(x+1\right)}{-6\left(x+2\right)}=\dfrac{2\left(x+1\right)}{3\left(x+2\right)^2}\)
b, \(A=\dfrac{2\left(x+1\right)}{3\left(x+2\right)^2}>0\)
\(\Leftrightarrow2x+2>0\) (vì \(3\left(x+2\right)^2\ge0\forall x\))
\(\Leftrightarrow x>-1\).
-Vậy \(x\in\left\{x\in Rlx>-1;x\ne2\right\}\) thì \(A>0\).
Đúng 1
Bình luận (0)
Cho biểu thức: K=(\(\dfrac{x^2}{x^2-5x+6}\)+\(\dfrac{x^2}{x^2-3x+2}\)).\(\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+x^2+1}\)
a, Tìm đkxđ rồi rút gọn K
b, Tìm GTLN của K
a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
Đúng 0
Bình luận (0)
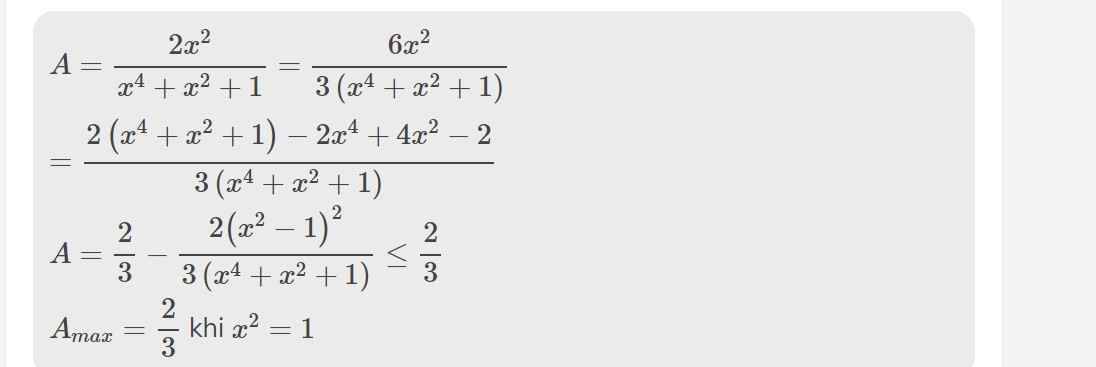
Tìm GTNN của biểu thức sau :
\(D=\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{3}\right|+\left|x+\dfrac{1}{4}\right|\)
\(D=\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{3}\right|+\left|x+\dfrac{1}{4}\right|\)
\(=\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{3}\right|+\left|-\left(x+\dfrac{1}{4}\right)\right|\)
\(=\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{3}\right|+\left|-x-\dfrac{1}{4}\right|\)
\(\ge x+\dfrac{1}{2}+0-x-\dfrac{1}{4}=\dfrac{1}{4}\)
Đẳng thức xảy ra khi \(x=-\dfrac{1}{3}\)
Vậy với \(x=-\dfrac{1}{3}\) thì \(D_{Min}=\dfrac{1}{4}\)
Đúng 0
Bình luận (0)
Ta có : | x + 1/2 | > hoặc = 0
| x + 1/3 | > hoặc = 0
| x + 1/4 | > hoặc = 0
=> D = | x + 1/2 | + | x + 1/3 | + | x + 1/4 | > hoặc = 0
Dấu " = " xảy ra khi D = 0
Vậy GTNN của biểu thức D là 0
Đúng 0
Bình luận (0)
Tìm GTLN của biểu thức: \(A=\left(\dfrac{x^2}{x^2-3x+2}+\dfrac{x^2}{x^2-5x+6}\right):\dfrac{x^4+x^2+1}{x^2-4x+3}\)
Bạn tham khảo lời giải tại đây:
Tìm GTLN của biểu thức: \(A=\left(\dfrac{x^2}{x^2-3x 2} \dfrac{x^2}{x^2-5x 6}\right):\dfrac{x^4 x^2 1}{x^2-4x 3}\) - Hoc24
Đúng 1
Bình luận (0)