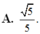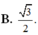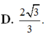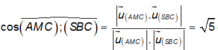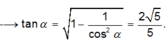cho hình vuông ABCD , gọi M là trung điểm AB . Tính góc AMC
PN
Những câu hỏi liên quan
cho abcd la hình chữ nhật có diện tích bằng 12dm vuông. Gọi m là trung điểm của ab tính diện tích hình tam giác amc
Tự vẽ hình nhá :))
*Nối MC
Số đo cạnh AM là : 12 : 2 = 6 (dm)
Vì 12 dm2 = 1 x 12 mà nửa AB đã là 6 dm => Chiều dài = 12,chiều rộng là 1
Diện tích hình tam giác AMC là : 6 x 1 : 2 = 3 dm2
Đ/s :....
( Mình ko chắc lắm )
Đúng 0
Bình luận (0)
Vì diện tích hình chữ nhật ABCD là 12dm2 nên thoả mãn điều kiện chiều dài là 3dm, chiều rộng là 4dm.
Vậy độ dài đáy hình tam giác AMC là:
4: 2 = 2 (dm)
Diện tích hình tam giác AMC là: 2* 3/2= 3 (dm2)
Đ/s: 3dm2
cho abcd la hình chữ nhật có diện tích bằng 12dm vuông. Gọi m là trung điểm của ab tính diện tích hình tam giác amc
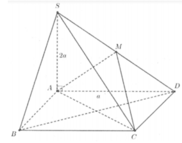
cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh AB=2a, SI vuông góc ( ABCD) vs I là trung điểm canh AB và SI=a√5. Gọi M là trung điểm của BC. a) CM BC vuông góc (SAB) và IM vuông góc (SBD) b) tính góc giữa SC và (ABCD)
Cho tam giác ABC ,góc A=90°,gọi M là trung điểm của BC ,gọi N là trung điểm của AB a, Cm:MN vuông góc AB b,Cm:tam giác AMC c,gọi D là điểm đối xứng với M qua N. Tứ giác ADBM là hình gì? Vì sao? d, tính chu vi tứ giác ADBM , Biết BC=8cm e, Tìm điều kiện của tam giác ABC để ADBM là hình vuông g, Tính diện tích hình vuông ADBM
a: Xét ΔBAC có BN/BA=BM/BC=1/2
nên MN//AC
=>MN vuông góc AB
b: ΔBAC vuông tại A
mà AM là trung tuyến
nên MA=MC
c: Xét tứ giác AMBD có
N là trung điểm chung của AB và MD
MA=MB
=>AMBD là hình thoi
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng A.
3
2
B.
2
3
3
C.
5...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng
A. 3 2
B. 2 3 3
C. 5 5
D. 2 5 5
Chọn D
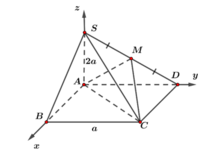
Để thuận tiện trong việc tính toán ta chọn a = 1.
Trong không gian, gắn hệ trục tọa độ Oxyz như hình vẽ sao cho gốc O trùng với điểm A, tia Ox chứa đoạn thẳng AB, tia Oy chứa đoạn thẳng AD, tia Oz chứa đoạn thẳng AS. Khi đó: A(0;0;0), B(1;0;0), C(1;1;0), S(0;0;2), D(0;1;0)
Vì M là trung điểm SD nên tọa độ là M 0 ; 1 2 ; 1
Ta có
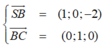
![]()
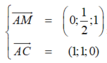
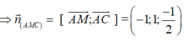
Gọi α là góc giữa hai mặt phẳng (AMC) và (SBC).
Suy ra
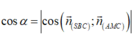
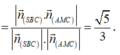
Mặt khác
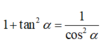
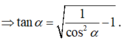
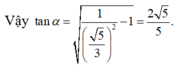
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA 2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng A.
5
5
B.
3
2
C.
2
5
5
D.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA =2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng
A. 5 5
B. 3 2
C. 2 5 5
D. 2 3 3
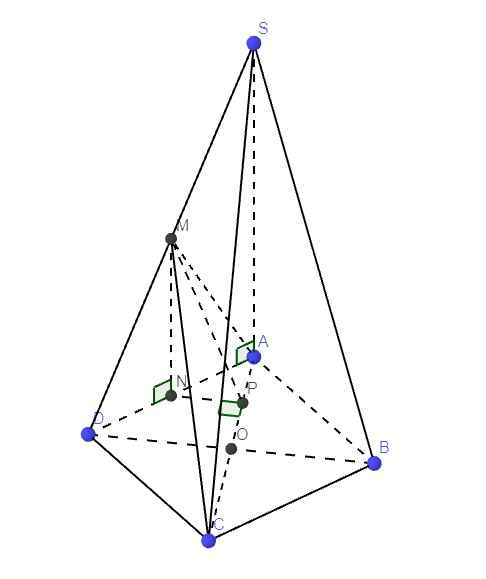
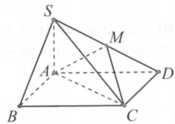
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc vs (ABCD), SB=SD= a căn 5 , gọi M là trung điên của SD. Tính góc giữa 2 mp (AMC) và (ABCD). Nếu đc thì vẽ giùm mình cái hình luôn ạ. Cảm ơn rất nhiều...
Gọi O là tâm đáy \(\Rightarrow OD\perp AC\) (đường chéo hình vuông)
Gọi N là trung điểm AD \(\Rightarrow\) MN là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}SA=\dfrac{a\sqrt{5}}{2}\\MN||SA\end{matrix}\right.\)
Do \(SA\perp\left(ABCD\right)\Rightarrow MN\perp\left(ABCD\right)\Rightarrow MN\perp AC\)
Gọi P là trung điểm AO \(\Rightarrow\) NP là đường trung bình tam giác OAD
\(\Rightarrow\left\{{}\begin{matrix}NP=\dfrac{1}{2}OD=\dfrac{a\sqrt[]{2}}{4}\\NP||OD\end{matrix}\right.\)
Mà \(OD\perp AC\Rightarrow NP\perp AC\)
\(\Rightarrow AC\perp\left(MNP\right)\)
Lại có AC là giao tuyến (AMC) và (ABCD)
\(\Rightarrow\widehat{MPN}\) là góc giữa (AMC) và (ABCD)
\(tan\widehat{MPN}=\dfrac{MN}{NP}=\sqrt{10}\Rightarrow\widehat{MPN}\approx72^027'\)
Đúng 0
Bình luận (0)
Cho hàm số S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên
S
A
2
a
và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng
A
M
C
và
S
B
C
bằng A.
5
5
.
B...
Đọc tiếp
Cho hàm số S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên S A = 2 a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng A M C và S B C bằng
A. 5 5 .
B. 3 2 .
C. 2 5 5 .
D. 2 3 3 .
Cho hàm số S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng
Đọc tiếp
Cho hàm số S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA=2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng