Chứng minh bất phương trình
A^2 +b^2 +c^2 +d^2 +4 >= 2*(a+b+c+d)
chứng minh các bất đẳng thức a^2+b^2+c^2+d^2+4 >=2.(a+b+c+d)
\(a^2+b^2+c^2+d^2+4\ge2\left(a+b+c+d\right)\)
\(a^2+b^2+c^2+d^2+4-2\left(a+b+c+d\right)\ge0\)
\(a^2+b^2+c^2+d^2+4-2a-2b-2c-2d\ge0\)
\(\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)+\left(d^2-2d+1\right)\ge0\)
\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2+\left(d-1\right)^2\ge0\)
Bất đẳng thức trên đúng với mọi a; b; c; d
=> bất đẳng thức được chứng minh
Cho a,b,c,d là các số thực. Chứng minh rằng a^2+b^2>=2ab(1). Áp dụng chứng minh các bất đẳng thức sau
a) (a^2+1)(b^2+1)(c^2+1)>=8abc
b) (a^2+4)(b^2+4)(c^2+4)(d^2+4)>=256abcd
a ) Áp dụng BĐT phụ \(a^2+b^2\ge2ab\) cho các cặp số thực , ta có :
\(\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)\ge2a.2b.2c=8abc\)
Dấu " = " xảy ra \(\Leftrightarrow a=b=c=1\)
b ) Làm tương tự như a )
Ta có: \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow a^2+b^2\ge2ab\)
a) Lại có : \(\left(a-1\right)^2\ge0\Leftrightarrow...\Leftrightarrow a^2+1\ge2a\)
cmtt \(\Rightarrow\left\{{}\begin{matrix}b^2+1\ge2b\\c^2+1\ge2c\end{matrix}\right.\)
Nhân vế theo vế ta đc: \(\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)\ge2a.2b.2c=8abc\left(dpcm\right)\)
b) Tiếp tục có \(\left(a-2\right)^2\ge0\Leftrightarrow...\Leftrightarrow a^2+4\ge4a\)
CMTT: \(\Rightarrow\left\{{}\begin{matrix}b^2+4\ge4b\\c^2+4\ge4c\end{matrix}\right.\)
Nhân vế theo vế ta đc: \(\left(a^2+4\right)\left(b^2+4\right)\left(c^2+4\right)\ge4a.4b.4c=256abc\left(dpcm\right)\)
Cho a,b,c,d là các số thực. Chứng minh rằng a^2+b^2>=2ab(1). Áp dụng chứng minh các bất đẳng thức sau
a) (a^2+1)(b^2+1)(c^2+1)>=8abc
b) (a^2+4)(b^2+4)(c^2+4)(d^2+4)>=256abcd
(a^2+b^2)/2>=ab
<=>(a^2+b^2)>=2ab
<=> a^2+2ab+b^2>=2ab
<=>a^2+b^2>=0(luôn đúng)
=> điều phải chứng minh.
Xét hiệu: \(a^2+b^2-2ab=\left(a-b\right)^2\ge0\)
=> \(a^2+b^2\ge2ab\)
Dấu "=" xra <=> a = b
Áp dụng ta có:
a) \(\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)\ge2a.2b.2c=8abc\)
dấu "=" xra <=> a = b = c = 1
b) \(\left(a^2+4\right)\left(b^2+4\right)\left(c^2+4\right)\left(d^2+4\right)\ge4a.4b.4c.4d=256abcd\)
Dấu "=" xra <=> a = b= c = d = 2
a) Áp dụng bđt AM-GM ta có:
\(\hept{\begin{cases}a^2+1\ge2a\\b^2+1\ge2b\\c^2+1\ge2c\end{cases}}\)
nhân theo 3 vế BDDT ta đc:
( a^2+1) (b^2+1)(c^2+1) >= 2a.2b.2c = 8abc
"=" <=> a=b=c
Tìm tập hợp nghiệm của bất phương trình:
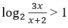
A. (- ∞ ; -2) B. (4; ∞ )
C. (- ∞ ; -2) ∪ (4; + ∞ ) D. (-2;4)
Tìm tập hợp nghiệm của bất phương trình: log 2 3 x x + 2 > 1
A. (- ∞ ; -2) B. (4; + ∞ )
C. (- ∞ ; -2) ∪ (4; + ∞ ) D. (-2;4)
cho A(-1, -2); B(2, -5); C(1, -2), D(-2, 1). chứng minh ABCD là hình bình hành. tìm hệ bất phương trình xác định mền trong của hình bình hành đó
Cho 4 số thực a,b,c,d bất kỳ chứng minh rằng: \(\sqrt{\left(a+c\right)^2+\left(b+d\right)^2}\le\sqrt{a^2+b^2}+\sqrt{c^2+d^2}\)
Sr chụy nha, em chưa học tới ~ :]]]
bdt tương đương với \(a^2+b^2+c^2+d^2+2ac+2bd\le a^2+b^2+c^2+d^2+2\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\)
\(\Leftrightarrow2\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\ge2\left(ac+bd\right)\)
\(\Leftrightarrow\sqrt{\left(a^2+b^2\right)\left(b^2+d^2\right)}\ge ac+bd\)
neu ac+bd \(\le0\) thi bdt can duoc cm
neu ac+bd \(\ge0\) thi \(\left(a^2+b^2\right)\left(c^2+d^2\right)\ge a^2c^2+b^2d^2+2abcd\)
\(\Leftrightarrow a^2c^2+a^2d^2+b^2c^2+b^2d^2\ge a^2c^2+b^2d^2+2abcd\)
\(\Leftrightarrow b^2c^2+a^2d^2-2abcd\ge0\Leftrightarrow\left(bc-ad\right)^2\ge0\left(dpcm\right)\)
Chứng minh: Với a,b,c,d bất kì ta có (a2+4)(b2+4)(c2+4)(d2+4) >= 256abcd
áp dụng AM-GM
a2+4>=4a
b2+4>=4b
c2+4>=4c
d2+4>=4d
nhân vế suy ra ĐPCM
Số nguyên lớn nhất thỏa mãn bất phương trình (x – 2)2 – x2 – 8x + 3 ≥ 0 là
A. x = -1
|
B. x = 0
|
C. x = 1
|
D. x = 2
|
Câu 41
Tập nghiệm của phương trình x + 1 = 5 là
A. 4
|
B. 4 ; - 6.
|
C. -4 ; 6.
|
D. -6
|
Câu 42
Số đo mỗi góc của lục giác đều là :
A. 1500.
|
B. 1080.
|
C. 1000.
|
D. 1200.
|
Câu 43
Phương trình nào sau đây là phương trình bậc nhất một ẩn ?
A. 0x + 25 = 0.
|
B. x + y = 0.
|
C.
|
D. 5x +
|
Câu 44
Tam giác ABC, có A B = 6 cm, AC = 8cm, BC = 10 cm, đường phân giác AD thì số đo độ dài đoạn BD và CD thứ tự bằng :
A. 3 ; 7.
|
B. 4 ; 6.
|
C.
|
D.
|
Câu 45
Trong các khẳng định sau, khẳng định nào không đúng
A. Hình hộp chữ nhật là hình lăng trụ đứng.
|
B. Các cạnh bên của hình lăng trụ đứng bằng nhau.
|
C. Hình lăng trụ đứng có đáy là hình bình hành là hình hộp chữ nhật.
|
D. Các mặt bên của hình lăng trụ đứng là hình chữ nhật.
|
Câu 46
Hãy chọn câu đúng.
A. Phương trình x = 0 và x(x + 1) là hai phương trình tương đương
|
B. kx + 5 = 0 là phương trình bậc nhất một ẩn số
|
C. Trong một phương trình ta có thể chuyển một hạng tử vế này sang vế kia đồng thời đổi dấu của hạng tử đó
|
D. Phương trình x = 2 và |x| = 2 là hai phương trình tương đương
|
Câu 47
Tam giác ABC, có A B = 3 cm, AC = 4cm, đường phân giác AD thì tỉ số hai đoạn BD và CD bằng :
A. 6.
|
B. 12.
|
C.
|
D.
|
Câu 48
Một hình chữ nhật có chu vi 20 m, nếu tăng chiều dài 2 m và tăng chiều rộng 1 m thì diện tích tăng 16 m2. Chiều dài của hình chữ nhật là:
A. 8 m.
|
B. 12 m
|
C. 6 m
|
D. 4 m
|
Câu 49
Số nghiệm của phương trình |2x – 3| - |3x + 2| = 0 là
A. 3
|
B. 2
|
C. 0
|
D. 1
|
Câu 50
Hình lập phương có diện tích toàn phần bằng 54cm2. Thì thể tích bằng?
A. 9 cm3.
|
B. 25 cm3.
|
C. 27 cm3.
|
D. 54 cm3. |
(x-2)^2 - x^2 - 8x+3 >= 0
x^2-4x+4 - x^2-8x +3 >=0
7>=12x
x<=12/7
x nguyên lớn nhất là 1