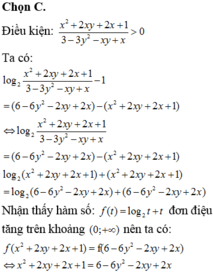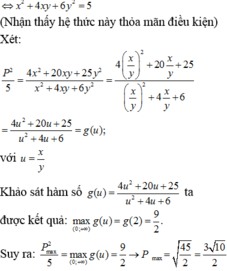Tìm giá trị của biểu thức : M=
DM
Những câu hỏi liên quan
Tìm giá trị của biểu thức : M= x−2yx+2y. Biết x-6y = xy .
Cho hai số thực x, y dương thỏa mãn:
log
2
x
2
+
2
x
y
+
2
x
+
1
3
-
3
y
2...
Đọc tiếp
Cho hai số thực x, y dương thỏa mãn: log 2 x 2 + 2 x y + 2 x + 1 3 - 3 y 2 - x y + x = 6 - x 2 - 4 x y - 6 y 2 Giá trị lớn nhất của biểu thức P=2x+5y bằng
![]()
![]()
![]()
Bài 6: Cho biểu thứ M = x2 – 2y + 3xy. Tính giá trị của M khi x = 2, y = 3
Bài 7: Cho biểu thức P = -x2 - 5xy + 8y2 . Tính giá trị của M tại x = -1 và y = -2
Bài 8: Tính giá trị biểu thức
A = 3x3 y + 6x2y2 + 3xy3 tại
B = x2 y2 + xy + x3 + y3 tại x = –1; y = 3
Bài 6:
M= 2.2 - 2.3+3.2.3
M= 4 - 6 + 18
M= 20
Bài 7:
P= 1.2 - 5.-1.-2 + 8.-2.2
P = 2 -10 -32
P= -44
Bài 8:
A (thiếu dữ kiện bn ơi)
B= -1.2 . 3.2 + -1.3 +3.3 +-1.3
B= -2 . 6 + -3 + 9 +-3
B= -2 . 6 - 3 + 9 - 3
B= -12 - 3 + 9 - 3
B= -9
Đúng 1
Bình luận (0)
Tìm các cặp số (x,y) để biểu thức -x2-y2+xy+2x+2y có giá trị lớn nhất
Tính giá trị của biểu thức
P
x
2
+
y
2
-
x
y
+
1
biết rằng
4
x
2
+
1
x
2
-
1
log
2...
Đọc tiếp
Tính giá trị của biểu thức P = x 2 + y 2 - x y + 1 biết rằng 4 x 2 + 1 x 2 - 1 = log 2 14 - y - 2 y + 1 với x ≠ 0 ; - 1 ≤ y ≤ 13 2 .
A. P = 4
B. P = 2
C. P = 1
D. P = 3
Đáp án B
Ta có x 2 + 1 x 2 - 1 ≥ 2 x 2 . 1 x 2 - 1 = 1 ⇒ 4 x 2 + 1 x 2 - 1 ≥ 4 14 - y - 2 y + 1 ≤ 16 ⇒ log 2 14 - y - 2 y + 1 ≤ 4
Theo giả thiết 4 x 2 + 1 x 2 - 1 = log 2 14 - y - 2 y + 1 ⇒ x 2 = 1 x 2 y = 0 ⇔ x 2 = 1 y = 0
Vậy giá trị biểu thức P = x 2 + y 2 - x y + 1 = 2 .
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất: A = x2 - 2xy + 6y2 - 12x +2y + 45
gọi x1 ;x2 là hai giá trị của x ;y1 và y2 là các giá trị tương ứng của y tìm x1 và x2 biết y1=6y2 và y1-y2=15
y1=6y2
y1-y2=15
=>y1=18; y2=3
x và y tỉ lệ nghịch
nên x1y1=x2y2
=>x1*18=x2*3
=>x1*6=x2*1
=>x2=6x1
Đúng 0
Bình luận (0)
Bài 3 :
a) Tìm x biết: (x+2)2 +(x+8)(x+2)
b) Tính giá trị biểu thức : B= (x+y)(x2 – xy + y2) –y3, tại x =10, y = 2021
Bài 3 :
a) Tìm x biết: (x+2)2 +(x+8)(x+2)
b) Tính giá trị biểu thức : B= (x+y)(x2 – xy + y2) –y3, tại x =10, y = 2021
Tính giá trị biểu thức:a) Q (3x – 1)(9
x
2
– 3x + 1) – (1 – 3x)(1 + 3x + 9
x
2
) tại x 10;b*)
P
x
4
3
+
y
2
3
biết xy 4 và x + 2y 8.
Đọc tiếp
Tính giá trị biểu thức:
a) Q = (3x – 1)(9 x 2 – 3x + 1) – (1 – 3x)(1 + 3x + 9 x 2 ) tại x = 10;
b*) P = x 4 3 + y 2 3 biết xy = 4 và x + 2y = 8.
a) Rút gọn Q = 54 x 3 , thay x = 10 vào tính được Q = 54000;
b) Gợi ý x 4 + y 2 = x + 2 y 4 = 8 4 = 2 . Kết quả P = 2.
Đúng 0
Bình luận (0)
Cho x+y=4 và x2+y2=10. Tính giá trị của biểu thức M=x6+y6
Cho 8x3-32y-32x2y+8x=0 và y khác 0. Tính giá trị của biểu thức M=3x+2y/3x-2y
Cho x2-5x+1=0 . Tính giá trị của biểu thức M=x4+x21/2x2
Giải giúp mình với!!!
Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
Đúng 2
Bình luận (0)
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$
Đúng 2
Bình luận (0)
Bài cuối $x^21$ không rõ. Bạn xem lại.
Đúng 1
Bình luận (0)