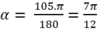Đổi số đo của các góc sau đây ra rađian :
a) \(18^o\)
b) \(57^o30'\)
c) \(-25^0\)
d) \(-125^045'\)
SK
Những câu hỏi liên quan
Đổi số đo của các số sau đây ra radian
a. 18°
b.57°30’
c. – 25°
d. -125°45’
a) Đổi từ độ sang rađian các số đo sau: \({360^ \circ }, - {450^ \circ }\)
b) Đổi từ rađian sang độ các số đo sau: \(3\pi , - \frac{{11\pi }}{5}\)
a) Ta có:
\(\begin{array}{l}{360^ \circ } = 360.\frac{\pi }{{180}} = 2\pi \\ - {450^ \circ } = 450.\frac{\pi }{{180}} = \frac{5}{2}\pi \end{array}\)
b)\(3\pi = 3\pi .{\left( {\frac{{180}}{\pi }} \right)^ \circ } = {540^ \circ }\)
\( - \frac{{11\pi }}{5} = \left( { - \frac{{11\pi }}{5}} \right).{\left( {\frac{{180}}{\pi }} \right)^ \circ } = - {396^ \circ }\)
Đúng 0
Bình luận (0)
Đổi số đo của các cung sau ra rađian (chính xác đến 0,001): 137 ο
Đổi số đo của các cung sau ra rađian (chính xác đến 0,001): - 78 ο 35 '
Đổi số đo của các cung sau ra rađian (chính xác đến 0,001): 26 ο
NT
24 tháng 7 2023 lúc 12:40
Đổi số đo của các góc sau đây sang radian:
a) −125°;
b) 42°;
\(a,-125^o=\dfrac{\pi.\left(-125\right)}{180}rad=-\dfrac{25\pi}{36}rad\\ b,42^o=\dfrac{\pi.42}{180}rad=\dfrac{7\pi}{30}rad\)
Đúng 2
Bình luận (0)
a, 25/35 \(\pi\)
b, 7/30 \(\pi\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Đổi số đo của các cung sau ra rađian (chính xác đến \(0,001\))
a) \(137^0\)
b) \(-78^035'\)
c) \(26^0\)
a) \(137^0\approx2,391\)
b) \(-78^035'\approx-1,371\)
c) \(26^0\approx0,454\)
Đúng 0
Bình luận (0)
Góc có số đo 1200 đổi sang rađian là góc
Chọn D.
Áp dụng công thức đổi độ ra rad 
Do đó 
Đúng 0
Bình luận (0)
Đổi số đo góc 1050 sang rađian bằng
Chọn B.
Áp dụng công thức đổi độ sang rad 
Do đó 
Đúng 0
Bình luận (0)