(d1): (m+1)x + (m-1)y -3=0
(d2): mx - y = 0
Tính góc (d1; d2)
LN
Những câu hỏi liên quan
Cho 2 đường thẳng: (d1) mx - y = 1 ; (d2) 2x + y = 3
a. tìm m để (d1) cắt (d2)
b. tìm m để (d1) cắt (d2) tại A(x;y) sao cho x > 0; y > 0
Cho đồ thị hàm số (d1) : y mx+3 và (d2) : y dfrac{-1}{m}x+3 (m≠0)a) Với m1. Vẽ các đồ thị (d1), (d2) trên cùng một mặt phẳng tọa độ và tìm tọa độ giao điểm của (d1) cắt (d2).b) Gọi A là giao điểm của (d1) và (d2); B và C lần lượt là giao điểm của (d1) và (d2) với trục hoành. Tìm m để diện tích tam giác ABC nhỏ nhất. Tính diện tích nhỏ nhất đó.
Đọc tiếp
Cho đồ thị hàm số (d1) : y= mx+3 và (d2) : y= \(\dfrac{-1}{m}\)x+3 (m≠0)
a) Với m=1. Vẽ các đồ thị (d1), (d2) trên cùng một mặt phẳng tọa độ và tìm tọa độ giao điểm của (d1) cắt (d2).
b) Gọi A là giao điểm của (d1) và (d2); B và C lần lượt là giao điểm của (d1) và (d2) với trục hoành. Tìm m để diện tích tam giác ABC nhỏ nhất. Tính diện tích nhỏ nhất đó.
Cho đồ thị hàm số (d1) : y mx+3 và (d2) : y dfrac{-1}{m}x+3 (m≠0)a) Với m1. Vẽ các đồ thị (d1), (d2) trên cùng một mặt phẳng tọa độ và tìm tọa độ giao điểm của (d1) cắt (d2).b) Gọi A là giao điểm của (d1) và (d2); B và C lần lượt là giao điểm của (d1) và (d2) với trục hoành. Tìm m để diện tích tam giác ABC nhỏ nhất. Tính diện tích nhỏ nhất đó.
Đọc tiếp
Cho đồ thị hàm số (d1) : y= mx+3 và (d2) : y= \(\dfrac{-1}{m}\)x+3 (m≠0)
a) Với m=1. Vẽ các đồ thị (d1), (d2) trên cùng một mặt phẳng tọa độ và tìm tọa độ giao điểm của (d1) cắt (d2).
b) Gọi A là giao điểm của (d1) và (d2); B và C lần lượt là giao điểm của (d1) và (d2) với trục hoành. Tìm m để diện tích tam giác ABC nhỏ nhất. Tính diện tích nhỏ nhất đó.
Tìm m, để:
a) 3 đường thẳng:
y=-5(x+1) (d1)
y=mx+3 (d2) ( phân biệt và đồng quy)
y=3x+m (d3)
b) (d) (2m-8)x+(m+2)y+m+1=0 và (d'): (8+2m)x+(m-2)y+3m+1=0 vuông góc với nhau
Cho 2 đường thẳng (d1) và (d2) lần lượt có phương trình : mx+(m-1)y-2(m+2)=0 và 3mx-(3m+1)y-5m-4=0 . Khi m=1/3 thì (d1) và (d2) ?
1.(D1) :y=x 1;(D2);y=-x+m;(D3):y=3x
2.(D1):y=2x;(D2):y=-x-3;(D3):y=mx+5
tìm m để 3 đường thẳng đồng qui
(d1) 2x-y+3=0
(d2) x+y+3=0
(d3) mx-y-1=0
Cho ba đường thẳng
d
1
:
x
−
2
y
+
1
0
,
d
2
:
m
x
−
3
m
−
2
y
+
2
m
−
2
0
,
d
3
:
...
Đọc tiếp
Cho ba đường thẳng d 1 : x − 2 y + 1 = 0 , d 2 : m x − 3 m − 2 y + 2 m − 2 = 0 , d 3 : x + y − 5 = 0 . Giá trị m để hai đường thẳng d1;d2 cắt nhau tại một điểm nằm trên d3 là
A.m = 0
B.m = 1
C.m = 2
D. không tồn tại m thỏa mãn
Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D
Đúng 0
Bình luận (0)
Cho 3 đường thẳng d1 : 2x+ y -1= 0 ; d2 : x+ 2y+1= 0 và d3 : mx-y-7= 0 Để ba đường thẳng này đồng qui thì m bằng ?
A. m= -6
B. m= 6
C.m= 3
D. m= 2
Đáp án B
+Giao điểm của d1 và d2 là nghiệm của hệ:
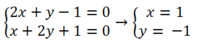
Vậy 2 đường thẳng d1 và d2 tại A( 1 ; -1) .
+Để 3 đường thẳng đã cho đồng quy thì d3 phải đi qua điểm A nên tọa độ A thỏa phương trình d3
Suy ra : m+ 1-7= 0 hay m= 6.
Đúng 0
Bình luận (0)