Vẽ và nêu cách vẽ
a) Góc AMB
b) Tia phân giác MC của AMB
NL
Những câu hỏi liên quan
Cho hình vẽ biết xx' \\yy' xAn^=42 độ a) Tính góc x'AB b) Vẽ tia phân giác cura ABy' cắt xx' tại M tính góc AMB c) Vẽ Bt là tia phân giác của góc mBy Chứng minh BM và Bt là 2 tia đối nhau d) vẽ ap là phân giác của góc x'ab cmr ap vuông góc với bm
Mình cần gấp lắm! Nhanh giúp mình
Cho Tam giác ABC có BC =10cm,trên BC vẽ điểm M sao cho 2BM=3MC
a, Tính đoạn BM vàMC
b,Vẽ tia Mx là tia phân giác của góc AMB và tia Mỹ là tia phân giác của góc AMC.CM rằng góc xMy = 90độ
c, Trên BC vẽ 2021điểm khác B,C,M tính số tam giác có đỉnh là A
b) Ta có: \(\widehat{AMx}=\dfrac{\widehat{AMB}}{2}\)(Mx là tia phân giác của \(\widehat{AMB}\))
\(\widehat{AMy}=\widehat{\dfrac{AMC}{2}}\)(My là tia phân giác của \(\widehat{AMC}\))
Do đó: \(\widehat{AMx}+\widehat{AMy}=\dfrac{\widehat{AMB}}{2}+\dfrac{\widehat{AMC}}{2}=\dfrac{\widehat{BMC}}{2}=\dfrac{180^0}{2}\)
hay \(\widehat{xMy}=90^0\)(đpcm)
Đúng 2
Bình luận (0)
a) Ta có: 2BM=3MC
nên \(BM=\dfrac{3}{2}MC\)
Ta có: BM+CM=BC(điểm M nằm giữa hai điểm B và C)
nên \(\dfrac{3}{2}MC+MC=10\)
\(\Leftrightarrow\dfrac{5}{2}MC=10\)
hay \(MC=10:\dfrac{5}{2}=10\cdot\dfrac{2}{5}=4\left(cm\right)\)
Ta có: MC+MB=BC(điểm M nằm giữa hai điểm B và C)
nên BM=BC-MC=10-4=6(cm)
Vậy: BM=6cm; MC=4cm
Đúng 1
Bình luận (0)
Vẽ tam giác ABM có AB = 5cm, BM = AM = 6,5cm;
Vẽ tiếp góc Amx kề bù với góc AMB;
Vẽ tam giác AMC, sao cho MA = MC và điểm C thuộc tia Mx;
So sánh MB, MA, MC;
Cho biết độ dài của đoạn thẳng BC;
Đo và cho biết số đo của góc BAC;
Đo và cho biết độ dài của đoạn thẳng AC
Sau khi ta vẽ được hình bs.21
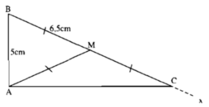
Ta có MA = MB = MC = 6,5cm
Do C thuộc tia đối của tia MB nên điểm M ở giữa hai điểm B, C đồng thời MB = MC = 5,6cm nên M là trung điểm của BC. Từ đó BC = 13cm.
Dùng thước đo góc, ta có ∠(BAC) = 90o
Sau khi đo đoạn thẳng AC có độ dài là 12cm
Đúng 0
Bình luận (0)
cho đường tròn tâm o bán kính r, đường kính AB vẽ dây AM bằng r
a) Tính các góc tam giác AMB và MB theo r
b) Vẽ tia phân giác MD của tam giác AMB .Gọi E,F là chân đường vuông góc vẽ từ D đến MA,MB .Tứ giác MEDF là hình gì ?vì sao? tính chu vi và diện tích của nó theo r
cho điểm Mnằm ngoài đường thẳng a,trên đường thẳng a lấy các điểm A,B,C sao cho góc AMB=68 độ,BMC=56 độ
a)vẽ tia MD là tia phân giác của góc AMB(Dthuộc đường thẳng a).tính góc DMC
a) Do D là phân giác góc AMB nên \(\widehat{DMB}=\frac{\widehat{AMB}}{2}=\frac{68^o}{2}=34^o\)
Vậy thì \(\widehat{DMC}=\widehat{DMB}+\widehat{BMC}=34^o+56^o=90^o\)
Đúng 0
Bình luận (0)
cho tam giác ABC với AB<AC,tia phân giác góc A cắt BC tại M.Chứng Minh rằng: góc AMC>góc AMB,
MC>MB,
góc AMB là góc nhọn
a:AB<AC
=>góc C<góc B
góc BAM+góc B+góc AMB=góc CAM+góc C+góc AMC
mà góc BAM=góc CAM; góc B>góc C
nên góc AMB<góc AMC
b: Xét ΔABC có AM là phân giác
nên MB/AB=MC/AC
mà AB<AC
nên MB<MC
c: góc AMB<góc AMC
=>góc AMB<1/2(góc AMB+góc AMC)=90 độ
=>góc AMB nhọn
Đúng 0
Bình luận (0)
Bài 1:
a) Vẽ tam giác AMB biết AB=6 cm, AM=BM=5 cm. (Nêu rõ cách vẽ)
b) Trong hình vẽ trên vẽ tam giác AMC sao cho góc AMB và góc AMC kề bù đồng thời CM=BM.Tính độ dài BC
c) Hãy vẽ đường tròn (M;5 cm). Cho biết đường tròn (M; 5 cm) đi qua những điểm nào? Giải thích tại sao?
Cách vẽ
Vẽ đoạn thẳng AB= 6 cm
Vẽ cung tròn A, bán kính 5 cm
Vẽ cung tròn B,bán kính 5 cm
Lấy một điểm giao cung trên gọi là điểm M
Vẽ MA , MB ta có ABC
Đúng 0
Bình luận (0)
Lần đầu vẽ hình t
Thông cảm
Đúng 0
Bình luận (0)
a) Vẽ tam giác ABM có AB = 5cm, BM = AM = 6,5 cm
b) Vẽ tiếp góc AMx kề bù với góc AMB
c) Vẽ tam giác AMC, sao cho MA = MC và điểm C thuộc tia Mx
d) So sánh MB, MA, MC
e) Cho biết độ dài của đoạn thẳng BC
f) Đo và cho biết số đo của góc BAC
g) Đo và cho biết độ dài của đoạn thẳng AC
Ta có MA = MB = MC = 6,5cm
Do C thuộc tia đối của tia MB nên điểm M ở giữa hai điểm B, C đồng thời MB = MC = 5,6cm nên M là trung điểm của BC. Từ đó BC = 13cm.
Dùng thước đo góc, ta có ∠(BAC) = 90o
Sau khi đo đoạn thẳng AC có độ dài là 12cm.
Đúng 0
Bình luận (0)
cho góc AMB=70 độ. Vẽ tia MC và MD lần lượt là tia đối của các tia MA và MB. Tính số đo góc CMD và góc AMD
góc CMD =70o(góc đối đỉnh của góc AMB)
góc AMD =20o (90o-70o)(bù nhau)
Cho tam giác ABC vuông tại A. Tia phân giác 𝐵 cắt cạnh AC tại D.
Bx là tia đối của tia BA. Vẽ By là tia phân giác của góc 𝑥𝐵𝐶 . Qua A vẽ đường thẳng vuông góc với BD cắt cạnh BC tại M.
a) CMR: By//AM
b) CMR: 𝐵𝐴𝑀 = 𝐵𝑀𝐴
c) Đường thẳng vuông góc với DB tại D cắt BC tại N.
CMR: 𝑁𝐷𝐶 + 𝑥𝐵𝑦 = 900
a: \(\widehat{yBC}=\dfrac{\widehat{xBC}}{2}\)
\(\widehat{DBC}=\dfrac{\widehat{CBA}}{2}\)
Do đó: \(\widehat{DBy}=90^0\)
\(\Leftrightarrow By\perp BD\)
hay By//AM
Đúng 1
Bình luận (0)