Không tính góc a.Tính tỉ số lượng giác góc a biết cotga=40/9
Câu1: hãy tính các tỉ số lượng giác còn lại của góc a, biết:
a) sin a =0,8, b) cos a =5/13 , c) tga =4/5 , d) cotga =3
Câu 2: Cho tam giác ABC vuông tại A. Tìm các tỉ số lượng giác cảu góc B khi:
a) BC = 5cm, AB = 3cm
b) BC = 13cm, AC = 12cm
c) AC = 4cm, AB = 3cm
Câu 3: Cho tam giác ABC. Biết AB = 40cm, AC = 58 cm và BC =42cm.
a) Tam giác ABC là tam giác gì ? vì sao ?
b) Kẻ đường cao BH cảu tam giác ABC. Tính độ dài đoạn thẳng BH.
c) Tính tỉ số lượng giác cảu góc A. Từ đó, suy ra tỉ số lượng giác của góc C.
Câu 4: Cho tam giác DEF vuông tại D, đường cao DH. Biết DE = 7cm và EF = 25cm.
a) Tính độ dài của các đoạn thẳng DF,DH,EH và HF.
b) Tính tỉ số lượng giác của góc F.
Cho tam giác ABC vuông cân tại A có cạnh góc vuông=a.Tính tỉ số lượng giác góc B
Lời giải
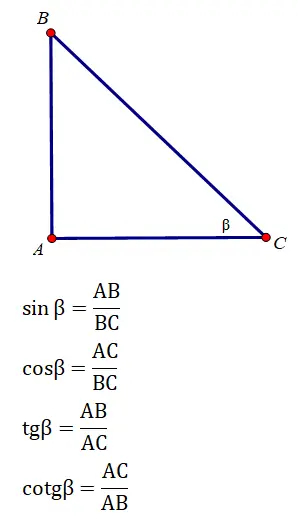
Các tỉ số lượng giác của góc β là:
mik nhầm nhé
Theo pitago thì BC= căn 2a^2 = căn 2 . a
Khi đó sinB = a/căn 2 . a = căn 2
cosB = sinB = căn 2
tanB = a/a = 1
cotB = tan B = 1
Vậy ta có : ...
xong
* Tính ( không dùng máy tính)
\(\sin^235^0+tan22^0+sin^255^0-cotg13^0:tan77^0-cotg68^0\)
* Cho góc nhọn a, sina=\(\dfrac{2}{3}\)biết. Không tính số đo góc, hãy tính cosa, tân, cotga
Bài 2:
\(\cos\alpha=\sqrt{1-\dfrac{4}{9}}=\dfrac{\sqrt{5}}{3}\)
\(\tan\alpha=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
\(\cot\alpha=\dfrac{\sqrt{5}}{2}\)
Cho tam giác vuông cân tại A.Có cạnh góc vuông=a.Tính tỉ số lượng giác góc B
10, Cho t/giác ABC vuông tại A có ^ABC= 40. Tính tỉ số lượng giác của ABC.
14, Cho α = 2. Tính các lượng giác còn lại của góc α biết góc α là góc nhọn.
chỉ rõ hộ mk từng cách giải đc ko ạ?
Cho góc nhọn α. Tính tỉ số lượng giác còn lại nếu cotα= 40/9
\(cot\alpha=\dfrac{40}{9}\Rightarrow tan\alpha=\dfrac{1}{cot\alpha}=\dfrac{1}{\dfrac{40}{9}}=\dfrac{9}{40}\)
+) \(\dfrac{1}{cos^2\alpha}=1+tan^2\alpha\)
\(\Leftrightarrow\dfrac{1}{cos^2\alpha}=1+\left(\dfrac{9}{40}\right)^2\\ \Rightarrow cos\alpha=\sqrt{1:\left(1+\left(\dfrac{9}{40}\right)^2\right)}=\dfrac{40}{41}\)
+) \(sin^2\alpha=1-cos^2\alpha\)
\(\Leftrightarrow sin\alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-\left(\dfrac{40}{41}\right)^2}=\dfrac{9}{41}\)
cho tam giác MNS có góc N =90 độ biết tan góc M = căn 3 . tính tỉ số lượng giác của góc M và góc S ( không dùng bảng số máy tính )
Bài 1 : cho tam giác ABC vuông tại A , AB = 6 , góc B = alpha, biết tan alpha bằng 5/2 . Tính : a, Cạnh AC b, Cạnh BC Bài 2 : Cho tam giác MNP vuông tại P . Hãy viết các tỉ số lượng giác của góc M và góc N . Biết góc M = 40° .
Bài 1:
a) Ta có:
\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)
\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)
b) Áp dụng Py-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+15^2=261\)
\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)
Bài 2:
\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)
cho tam giác ABC vuông tại A biết góc B =56 độ tính tỉ số lượng giác của góc B từ đó suy ra các tỉ số lượng giá của góc C
Xét ΔABC vuông tại A có
\(sinB=sin56\simeq0,83\)
\(cosB=cos56\simeq0,56\)
\(tanB=tan56\simeq1,48\)
\(cotB=cot56\simeq0,67\)
Xét ΔABC vuông tại A có
\(cosC=sinB\simeq0,83\)
\(sinC=cosB\simeq-0,56\)
\(cotC=tanB=tan56\simeq1,48\)
\(tanC=cotB\simeq0,67\)