gia sử x1 x2 là nghiệm của pt ax2+bx+c=0. tìm py bậc 2 có nghiệm là 1/x12 va 1/x22
NM
Những câu hỏi liên quan
Cho pt bậc x2 - (3m-1)x + 2m2 + m - 1=0 (m là tham số)
a) Giải pt khi m= -1
b) Giả sử x12 , x22 là hai nghiệm pb của chương trình. Tìm m để B= x12 - x22 - 3x1x2 đạt min
a: Khi m=-1 thì phương trình sẽ là:
x^2-(-3-1)x+2-1-1=0
=>x^2+4x=0
=>x=0 hoặc x=-4
Đúng 0
Bình luận (0)
Bài 1: Cho pt ẩn x:x2 - 2(m + 1)x + m2 + 7 0 (1)a) Giải pt (1) khi m -1; m 3.b) Tìm m để pt (1) có nghiệm là 4. Tìm nghiệm còn lại. c) Tìm m để pt (1) có 2 nghiệm x1, x2 thỏa: * x12 + x22 0 * x1 - x2 0Bài 2: Cho pt ẩn x:x2 - 2x - m2 - 4 0 (1)a) Giải pt (1) khi m -2.b) Tìm m để pt (1) có 2 nghiệm x1, x2 thỏa mãn: * x12 + x22 20 * x13 + x23 56 * x1 - x2 10
Đọc tiếp
Bài 1: Cho pt ẩn x:
x2 - 2(m + 1)x + m2 + 7 = 0 (1)
a) Giải pt (1) khi m = -1; m = 3.
b) Tìm m để pt (1) có nghiệm là 4. Tìm nghiệm còn lại.
c) Tìm m để pt (1) có 2 nghiệm x1, x2 thỏa:
* x12 + x22 = 0
* x1 - x2 = 0
Bài 2: Cho pt ẩn x:
x2 - 2x - m2 - 4 = 0 (1)
a) Giải pt (1) khi m = -2.
b) Tìm m để pt (1) có 2 nghiệm x1, x2 thỏa mãn:
* x12 + x22 = 20
* x13 + x23 = 56
* x1 - x2 = 10
Bài 1:
a, Thay m=-1 vào (1) ta có:
\(x^2-2\left(-1+1\right)x+\left(-1\right)^2+7=0\\
\Leftrightarrow x^2+1+7=0\\
\Leftrightarrow x^2+8=0\left(vô.lí\right)\)
Thay m=3 vào (1) ta có:
\(x^2-2\left(3+1\right)x+3^2+7=0\\ \Leftrightarrow x^2-2.4x+9+7=0\\ \Leftrightarrow x^2-8x+16=0\\ \Leftrightarrow\left(x-4\right)^2=0\\ \Leftrightarrow x-4=0\\ \Leftrightarrow x=4\)
b, Thay x=4 vào (1) ta có:
\(4^2-2\left(m+1\right).4+m^2+7=0\\ \Leftrightarrow16-8\left(m+1\right)+m^2+7=0\\ \Leftrightarrow m^2+23-8m-8=0\\ \Leftrightarrow m^2-8m+15=0\\ \Leftrightarrow\left(m^2-3m\right)-\left(5m-15\right)=0\\ \Leftrightarrow m\left(m-3\right)-5\left(m-3\right)=0\\ \Leftrightarrow\left(m-3\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=5\end{matrix}\right.\)
c, \(\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2+7\right)=m^2+2m+1-m^2-7=2m-6\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow2m-6\ge0\Leftrightarrow m\ge3\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+7\end{matrix}\right.\)
\(x_1^2+x_2^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-2\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-2m^2-14=0\\ \Leftrightarrow2m^2+8m-10=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-5\left(ktm\right)\end{matrix}\right.\)
\(x_1-x_2=0\\ \Leftrightarrow\left(x_1-x_2\right)^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-4\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-4m^2-28=0\\ \Leftrightarrow8m=28=0\\ \Leftrightarrow m=\dfrac{7}{2}\left(tm\right)\)
Đúng 2
Bình luận (0)
Bài 2:
a,Thay m=-2 vào (1) ta có:
\(x^2-2x-\left(-2\right)^2-4=0\\ \Leftrightarrow x^2-2x-4-4=0\\ \Leftrightarrow x^2-2x-8=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
b, \(\Delta'=\left(-m\right)^2-\left(-m^2-4\right)\ge0=m^2+m^2+4=2m^2+4>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-4\end{matrix}\right.\)
\(x_1^2+x_2^2=20\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow2^2-2\left(-m^2-4\right)=20\\ \Leftrightarrow4+2m^2+8-20=0\\ \Leftrightarrow2m^2-8=0\\ \Leftrightarrow m=\pm2\)
\(x_1^3+x_2^3=56\\ \Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=56\\ \Leftrightarrow2^3-3\left(-m^2-4\right).2=56\\ \Leftrightarrow8-6\left(-m^2-4\right)-56\\ =0\\ \Leftrightarrow8+6m^2+24-56=0\\ \Leftrightarrow6m^2-24=0\\ \Leftrightarrow m=\pm2\)
\(x_1-x_2=10\\ \Leftrightarrow\left(x_1-x_2\right)^2=100\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-100=0\\ \Leftrightarrow2^2-4\left(-m^2-4\right)-100=0\\ \Leftrightarrow4+4m^2+16-100=0\\ \Leftrightarrow4m^2-80=0\\ \Leftrightarrow m=\pm2\sqrt{5}\)
Đúng 0
Bình luận (0)
cho PT: x2-2mx 2m-2=0(1) m là tham số
a) GPT(1) khi m=1
b)CM: PT(1) luôn có 2 nghiệm x1, x2 với các giá trị nào của tham số m thì x12 x22=12c) với x1, x2 là 2 nghiệm của pt (1) , tìm giá trị lớn nhất của biểu thức A= 6(x1 x2)/x12 x12 4(x1 x2)
Cho phương trình: x2+mx+1=0 (1), m là tham số
a)Giải phương trình (1) khi m=4.
b)Tìm giá trị m để pt (1) có 2 nghiệm x1,x2 thõa mãn: x12/x22 + x22/x12 >7
Xem chi tiết
Bài 1: Cho pt ẩn x: x2 - 2(m+1) x + m2 - m 0 (1)a) Giải pt (1) khi m -1, m 0b) Tìm m để pt (1) có 1 nghiệm là 1. Tìm nghiệm còn lại. c) Trong trường hợp pt (1) có 2 nghiệm hãy tính: x12 + x22; (x1-x2)2.Bài 2: Cho pt: x2 - 4x + 3 0Tính giá trị biểu thức:a) x12 + x22b) dfrac{1}{x1+2}+dfrac{1}{x2+2}c) x13 + x23.d) x1 - x2.
Đọc tiếp
Bài 1: Cho pt ẩn x: x2 - 2(m+1) x + m2 - m = 0 (1)
a) Giải pt (1) khi m = -1, m = 0
b) Tìm m để pt (1) có 1 nghiệm là 1. Tìm nghiệm còn lại.
c) Trong trường hợp pt (1) có 2 nghiệm hãy tính: x12 + x22; (x1-x2)2.
Bài 2: Cho pt: x2 - 4x + 3 = 0
Tính giá trị biểu thức:
a) x12 + x22
b) \(\dfrac{1}{x1+2}+\dfrac{1}{x2+2}\)
c) x13 + x23.
d) x1 - x2.
Bài 2:
a: \(x^2-4x+3=0\)
=>x=1 hoặc x=3
\(x_1^2+x_2^2=1^2+3^2=10\)
b: \(\dfrac{1}{x_1+2}+\dfrac{1}{x_2+2}=\dfrac{1}{1}+\dfrac{1}{5}=\dfrac{6}{5}\)
c: \(x_1^3+x_2^3=1^3+3^3=28\)
d: \(x_1-x_2=1-3=-2\)
Đúng 0
Bình luận (0)
Cho phương trình
x
2
+
2
m
x
-
3
m
+
4
0
. Giả sử phương trình có hai nghiệm x1, x2. Lập phương trình bậc hai có các nghiệm là x12 và x22.
Đọc tiếp
Cho phương trình x 2 + 2 m x - 3 m + 4 = 0 . Giả sử phương trình có hai nghiệm x1, x2. Lập phương trình bậc hai có các nghiệm là x12 và x22.
![]()
![]()
![]()
![]()
Đáp án: D
Theo định lý Vi-ét ta có
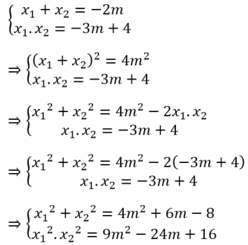
Khi đó, ![]() là nghiệm của phương trình
là nghiệm của phương trình
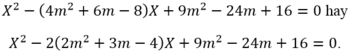
Đúng 0
Bình luận (0)
tìm các giá trị của m để pt x2-2mx+1=0 có nghiệm x1,x2 thỏa mãn x12 + x22 =8
PT có 2 nghiệm phân biệt`<=> \Delta' >0`
`<=> m^2-1>0`
`<=> m<-1 ; 1 <m`
Viet: `x_1+x_2=2m`
`x_1x_2=1`
Theo đề: `x_1^2+x_2^2=8`
`<=> (x_1+x_2)^2-2x_1x_2=8`
`<=> 4m^2-2=8`
`<=> 4m^2 - 10=0`
`<=>` \(\left[{}\begin{matrix}m=\dfrac{\sqrt{10}}{2}\\m=-\dfrac{\sqrt{10}}{2}\end{matrix}\right.\)
Vậy `m=\pm \sqrt10/2`.
Đúng 3
Bình luận (3)
`x_1^2+x_2^2 = (x_1^2+2x_1x_2+x_2^2)-2x_1x_2 = (x_1+x_2)^2-2x_1x_2`
Đúng 0
Bình luận (0)
Cho phương trình x2- mx + m –1 =0 ( 1)
a) Giải pt khi m = 4
b) Cho biết x1, x2 là hai nghiệm của pt (1). tính x1 + x2 ; x1 . x2 ; x12 + x22 ; x14+ x24
a: Khi m=4 thì phương trình trở thành \(x^2-4x+3=0\)
=>(x-3)*(x-1)=0
=>x=3 hoặc x=1
b: \(x_1+x_2=m\)
\(x_1x_2=m-1\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=m^2-2\left(m-1\right)=m^2-2m+2\)
\(x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2\left(x_1x_2\right)^2\)
\(=\left(m^2-2m+2\right)^2-2\cdot\left(m-1\right)^2\)
\(=m^4+4m^2+4-4m^3+4m^2-8m-2m^2+4m-2\)
\(=m^4-4m^3+2m^2-4m+2\)
Đúng 2
Bình luận (0)
Cho pt: x2 - (m + 2) + 7m - 2m2 - 3 = 0 (với x là ẩn số) (1)
a) Chứng tỏ phương trình (1) luôn có 2 nghiệm phân biệt.
b) Tìm m để phương trình (1) có hai nghiệm x1 , x2 thỏa hệ thức:
2(x12 - x22) - 5x1x2 = 2
phương trình bạn copy thiếu ak bạn ơi?
Đúng 0
Bình luận (3)




