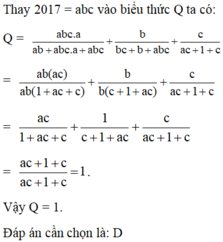cho a+b+c=a^3+b^3+c^3=1. tính giá trị của biểu thức P= a^2017+b^2017+c^2017
GN
Những câu hỏi liên quan
Cho các số thực a, b, c thỏa mãn a + b + c = 3 và 1/a + 1/b + 1/c = 1/3 . Tính giá trị biểu thức P = (a − 3)^2017 .(b − 3)^2017 .(c − 3)^2017
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{3} \Leftrightarrow \dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{a+b+c}(vì a+b+c=3)\)
\(\Leftrightarrow \dfrac{1}{a}+ \dfrac{1}{b}= \dfrac{1}{a+b+c}- \dfrac{1}{c }\)
\(\Leftrightarrow \dfrac{b+a}{ab}=\dfrac{c-a-b-c}{ac+bc+c^{2}}\)
\(\Leftrightarrow \dfrac{a+b}{ab}=\dfrac{a+b}{-ac-bc-c^2}\)
\(\Leftrightarrow \left[\begin{array}{} a+b=0\\ ab=-ac-bc-c^2 \end{array} \right.\)
\(\Leftrightarrow \left[\begin{array}{} a+b=0\\ ab+ac+bc+c^2=0 \end{array} \right.\)
\(\Leftrightarrow \left[\begin{array}{} a+b=0\\ (a+c)(b+c)=0 \end{array} \right.\)
\(\Leftrightarrow \left[\begin{array}{} a+b=0\\ a+c=0\\ b+c=0 \end{array} \right.\)
Vì vai trò của a,b,c là như nhau nên ta giả sử a+b=0
mà a+b+c=0
\(\Rightarrow c=3\)
Thay c=3 vào biểu thức P ta có:
\(P=(a-3)^{2017}.(b-3)^{2017}.(3-3)^{2017} =0 \)
Vậy P=0
Đúng 0
Bình luận (0)
Cho \(a^3+b^3+c^3=3abc\)
Tính giá trị biểu thức \(A=\frac{a^{2017}}{b^{2017}}+\frac{b^{2017}}{c^{2017}}+\frac{c^{2017}}{a^{2017}}\)
cm \(a^3+b^3+c^3=3abc\)
thì \(\orbr{\begin{cases}a+b+c=0\\a=b=c\end{cases}}\)
(chuyển vế xét hiệu )
Đúng 0
Bình luận (0)
TA CÓ: \(a^3+b^3+c^3=3abc\)
\(\Rightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
\(\Rightarrow a^2+b^2+c^2-ab-bc-ca=0\)
\(\Rightarrow2a^2+2b^2+2c^2=2ab+2bc+2ca\)
\(\Rightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Rightarrow a-b=0;c-a=0;b-c=0\Rightarrow a=b=c\)
\(\Rightarrow\frac{a^{2017}}{b^{2017}}+\frac{b^{2017}}{c^{2017}}+\frac{c^{2017}}{a^{2017}}=1+1+1=3\)
Đúng 0
Bình luận (0)
Cho a,b,c là các số dương thỏa mãn \(a^3+b^3+c^3=3abc\)
Hãy tính giá trị của biểu thức A = \(\frac{a^{2017}}{b^{2017}}+\frac{b^{2017}}{c^{2017}}+\frac{c^{2017}}{a^{2017}}\)
\(a^3+b^3+c^3=3abc\Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc=0\)
\(\Leftrightarrow\frac{\left(a+b+c\right)}{2}.\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\)
\(\Leftrightarrow a=b=c\) (a,b,c là các số dương)
Bạn thay vào A để tính.
Đúng 0
Bình luận (0)
Cho a,b,c là các số dương thỏa mãn a3+b3+c3=3abc
Hãy tính giá trị của biểu thức A = \(\frac{a^{2017}}{b^{2017}}\) +\(\frac{b^{2017}}{c^{2017}}\) +\(\frac{c^{2017}}{a^{2017}}\)
Năm sau em học lớp 8 em làm giùm cko
Đúng 0
Bình luận (0)
2 nam nx e len lp 8 e lm cho nha cj cho e nhe
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cả nhà ơi cho tớ hỏi với, đề thi kiểm tra toán trường tớ lớp 8. ai biết bày cho tớ với
a) tìm các giá trị nguyên dương x, y sao cho 3xy+x+y=17
b) cho 3 số a, b, c thỏa mãn a+b+c=1 và a^3+b^3+c^3=1
tính giá trị của biểu thức P=a^2017+b^2017+c^2017
~ mấy bạn ơi giúp tớ nhanh với, tớ gấp lắm ~
Kiểm tra mà bạn vẫn có thời gian đưa câu hỏi ư! Bái phục mà thi j vậy bn?
Đúng 0
Bình luận (0)
Cho các số nguyên a,b,c khác 0 thỏa mãn: ab+1=c(a-b+c).Tính giá trị của biểu thức A=\(\frac{2017.a-b}{2017.a+b}+\frac{2017.b-a}{2017.b+a}\)
Đúng cho 10tk
cho a, b, c là 3 số thực khác 0, thỏa mãn
\(\frac{a+b-2017\cdot c}{c}=\frac{b+c-2017\cdot a}{a}=\frac{c+a-2017\cdot b}{b}\)
tính giá trị của biểu thức
B=\(\left(1+\frac{b}{a}\right)\cdot\left(1+\frac{a}{c}\right)\cdot\left(1+\frac{c}{a}\right)\)
Cho a, b, c thỏa mãn abc 2017. Tính giá trị biểu thức sau
Q
2017a
ab
+
2017a
+
2017
+
b
bc
+
b
+
2017
+
c
ac
+
1
+...
Đọc tiếp
Cho a, b, c thỏa mãn abc = 2017. Tính giá trị biểu thức sau Q = 2017a ab + 2017a + 2017 + b bc + b + 2017 + c ac + 1 + c
A. Q = -1
B. Q = 0
C. Q = 2
D. Q = 1
Cho 3 số a,b,c thõa mãn a/2015 = b/2016 = c/2017. Tính giá trị biểu thức B=4*(a-b)*(b-c)*(c-a)^2