tìm giá trị nhỏ nhất của:
m2_4m.n+10m-22+32
Câu 21. Cho ![]() và
và ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức ![]()
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Câu 22. Tìm giá trị nhỏ nhất của ![]() .
.
A. ![]() đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là ![]() . B.
. B. ![]() đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là ![]()
C. ![]() đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là ![]() . D.
. D. ![]() đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là ![]() .
.
Câu 23. Tìm giá trị lớn nhất của ![]() .
.
A. ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]() . B.
. B. ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]()
C. ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]() . D.
. D. ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]() /
/
Câu 24. Tìm ![]() thỏa mãn
thỏa mãn ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 25. Hỏi có bao nhiêu giá trị ![]() thỏa mãn
thỏa mãn ![]() ?
?
A. Có một giá trị B. Có hai giá trị
C. Có ba giá trị D. Có bốn giá trị.
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
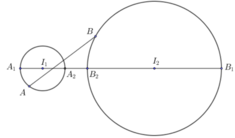
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8
tìm x để biểu thức M đạt giá trị nhỏ nhất và tìm giá trị nhỏ nhất đó:
M=(2x+5)^2 + 2x( 3x-4) - (x^2+22)
Tìm giá trị nhỏ nhất của biểu thức M = |x – 22| + |x + 12|
\(M=\left|x-22\right|+\left|x+12\right|\)
\(M=\left|22-x\right|+\left|x+12\right|\ge\left|22-x+x+12\right|\)
\(M=\left|22-x\right|+\left|x+12\right|\ge34\)
\(M\ge34\)
Dấu "\(=\)" xảy ra khi:
\(\left(22-x\right)\left(x+12\right)\ge0\)
\(TH1:22-x\ge0;x+12\ge0\)
\(\Rightarrow22\ge x\ge-12\)
\(TH2:22-x\le0;x+12\ge0\)
\(\Rightarrow22\le x;x\ge12\left(vô.lý\right)\)
Vậy \(GTNN\) của \(M\) là \(34\) khi \(22\ge x\ge-12\)
Dấu "" xảy ra khi:
Vậy của là khi
Tìm giá trị nhỏ nhất của biểu thức M = |x – 22| + |x + 12|
Áp dụng BĐT trị tuyệt đối:
\(M=\left|22-x\right|+\left|x+12\right|\ge\left|22-x+x+12\right|=34\)
Vậy \(M_{min}=34\) khi \(\left(22-x\right)\left(x+12\right)\ge0\Rightarrow-12\le x\le22\)
Tìm giá trị nhỏ nhất của phân thức B = 2 x 2 - 16 x + 41 x 2 - 8 x + 22
cho x>0 tìm giá trị nhỏ nhất \(x+\dfrac{32}{x^2}\)
\(x+\dfrac{32}{x^2}=\dfrac{x}{2}+\dfrac{x}{2}+\dfrac{32}{x^2}\ge3\sqrt[3]{\dfrac{x}{2}.\dfrac{x}{2}.\dfrac{32}{x^2}}=3\sqrt[3]{\dfrac{32}{4}}=6\)
\(Min=6\Leftrightarrow\dfrac{x}{2}=\dfrac{32}{x^2}\Leftrightarrow x^3=64\Leftrightarrow x=4\)
\(\Leftrightarrow x+\dfrac{\left(4\sqrt{2}\right)^2}{x^2}\Leftrightarrow x+\dfrac{4\sqrt{2}}{x}\)
ta có x>0
áp dụng BĐT Cô si ta có:
\(x+\dfrac{4\sqrt{2}}{x}\ge2\sqrt{x.\dfrac{4\sqrt{2}}{x}}\)
\(\Leftrightarrow x+\dfrac{4\sqrt{2}}{x}\ge2\sqrt{4\sqrt{2\simeq}4,75}\)
dấu = xảy ra khi x\(\simeq2,37\)
tìm giá trị nhỏ nhất của các biểu thức A=x^2-10x+32
\(A=x^2-10x+32=x^2-10x+25+9=\left(x-5\right)^2+9\)
mà \(\left(x-5\right)^2\ge0\)
\(\Rightarrow\left(x-5\right)^2+9\ge9\)
\(\Rightarrow Min\left(A\right)=9\)
Tìm m và p sao cho : A = m2 - 4mp =5p2 +10m -22p +28 đạt giá trị nhỏ nhất . Tính giá trị ấy
A = (m2 -4mp + 4p2 ) + (p2 -2p + 1) + 27 + 10m - 20p = (m-2p)2 + (p-1)2 27 + 10(m-2p)
Đặt X = m-2p.
Ta có A=x2 + 10X + 27 + (p-1)2 = (X2 + 10X + 25) + (p-1)2 + 2 = (X+5)2 + (p-1)2 + 2
Ta thấy: (X + 5)^2> 0 với m, p; (p-1)^2> 0 p Do đó: A đạt giá trị nhỏ nhất khi: Vậy Min A=2 khi m=-3; p=1
Có bài số ko hỏi tớ-_-