Phủ định tuyệt đối là j
Phủ định tương đối là j
Các địa chỉ cột và dòng được cố định khi ô chứa công thức được sao chép đến vị trí ô
khác thì gọi là địa chỉ?
A. Địa chỉ tương đối B. Địa chi tương đối dòng, tuyệt đối cột
C. Địa chỉ tuyệt đối D. Địa chi tuyệt đối dòng, tương đối cột
Không khí ở 25 ° C có độ ẩm tương đối là 70 % . Hãy xác định độ ẩm cực đại , và độ ẩm tuyệt đối của không khi ở 25ºC
Dựa vào bảng áp suất hơi bão hòa và khối lượng riêng của nước ta suy ra độ ẩm cực đại của không khí ở 250C là 23g/m3
Độ ẩm tuyệt đối: \(a=f.A=0,7.23=16,1g/m^3\)
Nhiệt độ của không khí là 300C. Độ ẩm tương đối là 64%. Hãy xác định độ ẩm tuyệt đối và điểm sương. (Tính các độ ẩm theo bảng tính chất hơi nước bão hòa).
Theo công thức độ ẩm tương đối: f = a A ⇔ a = f . A
Tra bảng ta có ở 300C: A = 30,3g/m3.
So sánh ta thấy ở nhiệt độ cỡ 220C thì độ ẩm cực đại là 19,4. Vậy điểm sương của không khí ở 300C này là 220C.
Nhiệt độ của không khí là 30 ° C . Độ ẩm tương đối là 64%. Hãy xác định độ ẩm tuyệt đối và điểm sương.
Chú ý: Tính các độ ẩm theo áp suất riêng phần
Theo bảng áp suất bão hòa của hơi nước ở các nhiệt độ khác nhau thì ở 30 ° C , áp suất hơi nước bão hòa là p b = 31 , 8 m m H g .
Độ ẩm tương đối tính theo tỉ số của áp suất riêng phần của hơi nước trong không khí và áp suất của hơi nước bão hòa ở cùng nhiệt độ: H = p h n p b % .
Theo đó, độ ẩm tuyệt đối thể hiện bằng áp suất riêng phần của hơi nước trong không khí là:
![]()
Điểm sương t s chính là nhiệt độ mà tại đó áp suất hơi bão hòa của nước là 20,35mmHg.
Trong bảng áp suất hơi nước bão hòa của nước ở các nhiệt độ khác nhau (SGK) không có giá trị nhiệt độ ứng với p b = 20 , 35 m m H g , mà có các giá trị gần với nó nhất
![]()
![]()
Có thể tính nhiệt độ t s ứng với p b = 20 , 35 m m H g bằng phương pháp nội suy:
Độ chênh lệch nhiệt độ ứng với khoảng chênh lệch áp suất trong khoảng từ t 1 đến t 2
![]()
![]()
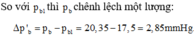
Độ chênh lệch nhiệt độ tương ứng:
![]()
![]()
Xác định độ cao tương đối và tuyệt đối của điểm A, B, C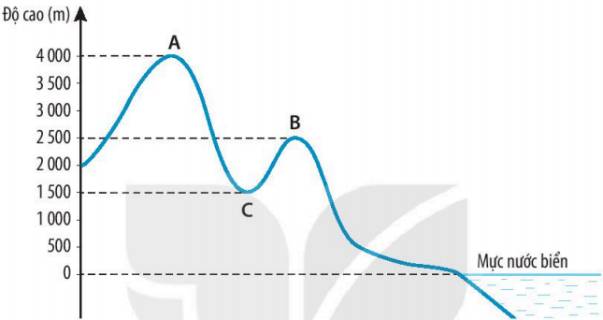
A - 4 000 m.
B. 2 500 m.
C. 1 500 m.
* Đối với điểm A:
- Độ cao tuyệt đối của điểm A: 4000m
- Độ cao tương đối của điểm A:
+ Điểm A so với điểm B: 1500m
+ Điểm A so với điểm C: 2500m
* Đối với điểm B:
- Độ cao tuyệt đối của điểm B: 2500m
- Độ cao tương đối của điểm B(Điểm B so với điểm C): 1000m
* Đối với điểm C:
- Độ cao tuyệt đối của điểm C: 1500m
Nhiệt độ tuyệt đối là gì? Viết công thức định luật Sác -lơ và đường đẳng tích tương ứng trong nhiệt giai Ken -vin.
Ken-vin đề xuất một nhiệt giai mang tên ông. Theo đó, khoảng cách nhiệt độ 1 Ken-vin (kí hiệu 1K) bằng khoảng cách 1 o C . Không độ tuyệt đối (0K) ứng với nhiệt độ 273 0 C .
Nhiệt độ đo trong nhiệt giai Ken-vin gọi là nhiệt độ tuyệt đối.
Gọi T là nhiệt độ trong nhiệt giai Ken-vin, còn t là số đo cùng nhiệt độ đó trong nhiệt giai Xen-xi-út thì: T= t + 273.
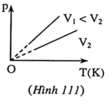
Trong nhiệt giai Ken-vin, công thức của định luật Sác-lơ là: P T = hằng số.
Đường đẳng tích (p, T) như hình 111. Đường đẳng tích là nửa đường thẳng có đường kéo dài đi qua gốc tọa độ. Ứng với các thể tích khác nhau của cùng một lượng khí có các đường đẳng tích khác nhau. Trên hình 105 đường đẳng tích ở trên ứng với thể tích nhỏ hơn đường ở dưới.
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.
Sai số tuyệt đối của phép đo:
Sai số tương đối của phép đo:
Kết quả phép đo:
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.
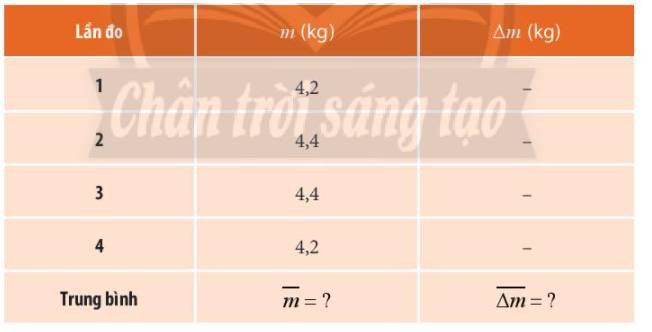
Sai số tuyệt đối của phép đo: \(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = ?\)
Sai số tương đối của phép đo: \(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = ?\)
Kết quả phép đo: \(m = \overline m \pm \Delta m = ?\)
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)
Xác định sai số tuyệt đối của số gần đúng a = 123456 biết sai số tương đối δa = 0,2%.
A. 123,456.
B. 0,0002.
C. 146,912.
D. 14691,2.
Đáp án: C
Sai số tuyệt đối là: Δa = |a|.δa = 123456. 0,2% = 146,912.