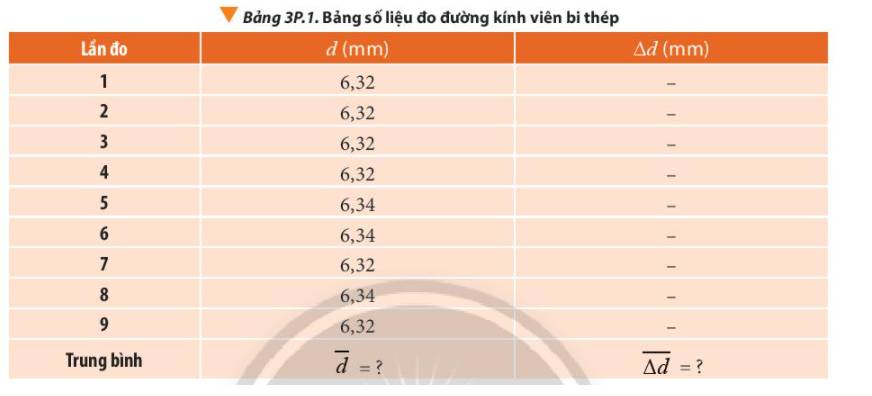
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.
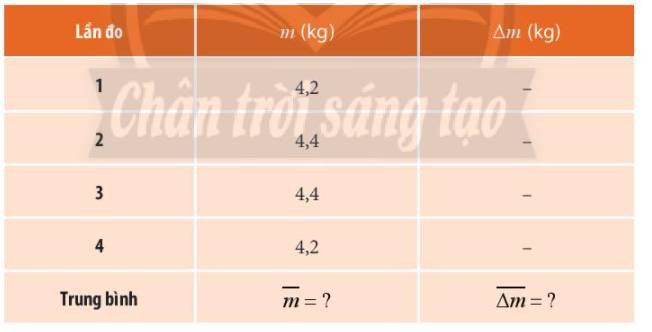
Sai số tuyệt đối của phép đo: \(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = ?\)
Sai số tương đối của phép đo: \(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = ?\)
Kết quả phép đo: \(m = \overline m \pm \Delta m = ?\)
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)