Chọn câu đúng . Giả sử \(\frac{x}{y}=4;x.y=9\) . Ngoài ra \(x\) lớn hơn hoặc bằng 0 . Khi đó (x;y) bằng :
A . (4 ; 1 ) B . (8;2) C. (3;3) D . (9;1) E . ( 6 ; \(\frac{3}{2}\))
LL
Những câu hỏi liên quan
Giả sử a; b; c là các số thực dương. Chọn câu đúng: A.
1
+
a
2
+
1
+
b
2
+
1
+
c
2
≤
2
a
+
b
+...
Đọc tiếp
Giả sử a; b; c là các số thực dương. Chọn câu đúng:
A. 1 + a 2 + 1 + b 2 + 1 + c 2 ≤ 2 a + b + b + c + c + a
B. 1 + a 2 + 1 + b 2 + 1 + c 2 ≥ 2 a + b + b + c + c + a
C. 1 + a 2 + 1 + b 2 + 1 + c 2 ≤ a + b + b + c + c + a
D. 1 + a 2 + 1 + b 2 + 1 + c 2 ≥ a + b + b + c + c + a
Cho hình thang cân ABCD (AB // CD). Giả sử
A
B
≤
C
D
, chọn câu đúng. A.
B
D
2
-
B
C
2
C
D
×
A
B
B.
B
D
2
-
B
C
2...
Đọc tiếp
Cho hình thang cân ABCD (AB // CD). Giả sử A B ≤ C D , chọn câu đúng.
A. B D 2 - B C 2 = C D × A B
B. B D 2 - B C 2 = A B 2
C. B D 2 - B C 2 = 2 C D × A B
D. B D 2 - B C 2 = B C × A B
Đáp án cần chọn là: A
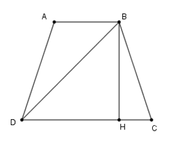
Kẻ BH ⊥ CD tại H.
Xét tam giác vuông BDH, theo định lý Pytago, ta có B D 2 = D H 2 + B H 2
Xét tam giác vuông CBH, theo định lý Pytago, ta có B C 2 = C H 2 + B H 2
Suy ra B D 2 - B C 2 = D H 2 + B H 2 - C H 2 + B H 2
= D H 2 - C H 2 = B H + D H × D H - B H = C D × A B
Đúng 0
Bình luận (0)
H24
23 tháng 1 2024 lúc 21:40
Một bài trắc nghiệm có 10 câu hỏi ,mỗi câu có 4 phương án lựa chọn trong đó có một đáp án đúng . Giả sử mỗi câu trả lời đúng được 5 điểm sai bị trừ 2 điểm . Một học sinh không học bài nên chọn ngẫu nhiên một phương án . Tính xác xuất để học sinh nhận điểm dưới 1
Giả sử học sinh đó chọn x câu đúng (với \(0\le x\le10\)), như vậy sẽ có \(10-x\) câu sai
Số điểm học sinh đó đạt được là:
\(5x-2\left(10-x\right)=7x-20\)
Điểm dưới 1 \(\Rightarrow7x-20< 1\Rightarrow x< 3\)
Vậy học sinh đó trả lời đúng 0,1 hoặc 2 câu
Xác suất đúng khi chọn mỗi câu hỏi là 1/4 còn xác suất sai là 3/4 nên xác suất học sinh đó dưới 1 điểm là:
\(C_{10}^0.\left(\dfrac{1}{4}\right)^0.\left(\dfrac{3}{4}\right)^{10-0}+C_{10}^1.\left(\dfrac{1}{4}\right)^1.\left(\dfrac{3}{4}\right)^{10-1}+C_{10}^2.\left(\dfrac{1}{4}\right)^2.\left(\dfrac{3}{4}\right)^{10-2}=...\)
Đúng 3
Bình luận (1)
Giả sử x = \(\frac{a}{m}\),y=\(\frac{b}{m}\)(a,b,m\(\varepsilon\)Z và m>0 ) và x<y.Hãy chứng tỏ rằng nếu chọn z= \(\frac{a+b}{2m}\)thì ta có x<z<y
bạn nào nhanh đúng mik tik cho chiu hog
Vì x < y nên \(\frac{a}{m}< \frac{b}{m}\) suy ra a < b
=> a + b > 2a => \(z=\frac{a+b}{2m}>\frac{2a}{2m}=\frac{a}{m}=x\) (1)
Từ a < b => a + b < 2b => \(z=\frac{a+b}{2m}< \frac{2b}{2m}=\frac{b}{m}=y\) (2)
Từ (1) ; (2) => x < z < y (đpcm)
Đúng 0
Bình luận (0)
Câu Hỏi TodayDễ : So sánh các số hữu tỉ Khó : Giả sử (a, b, m ∈ Z; m 0) và x y. Hãy chứng minh nếu chọn thì ta có x z y.
Đọc tiếp
Câu Hỏi Today
Dễ : So sánh các số hữu tỉ
Khó : Giả sử 
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 
thì ta có x < z < y.
Một đề thi trắc nghiệm có 12 câu hỏi, mỗi câu có 5 phương án, trong đó chỉ có một phương án đúng. Giả sử mỗi câu trảl ời đúng được 4 điểm còn mỗi câu trảlời sai bị trừ1 điểm. Một học sinh học kém không học gì làm bài bằng cách chọn hú họa một phương án trảl ời cho mỗi câu. Tính xác suất: a. Học sinh đó được 13 điểm.b. Học sinh đó bịđiểm âm.
Đọc tiếp
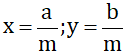
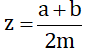
Một đề thi trắc nghiệm có 12 câu hỏi, mỗi câu có 5 phương án, trong đó chỉ có một phương án đúng. Giả sử mỗi câu trảl ời đúng được 4 điểm còn mỗi câu trảlời sai bị trừ1 điểm. Một học sinh học kém không học gì làm bài bằng cách chọn hú họa một phương án trảl ời cho mỗi câu. Tính xác suất:
a. Học sinh đó được 13 điểm.
b. Học sinh đó bịđiểm âm.
Câu Hỏi YESTERDAY AND TODAYDễ : So sánh các số hữu tỉ Khó : Giả sử (a, b, m ∈ Z; m 0) và x y. Hãy chứng minh nếu chọn thì ta có x z y
Đọc tiếp
Câu Hỏi YESTERDAY AND TODAY
Dễ : So sánh các số hữu tỉ
Khó : Giả sử
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
thì ta có x < z < y
a)11/11.x=-22/77 b)12/12.x=-216/300<-213/300
7/7.y=-21/77 x>y
=>x<y
c)-0,75=-3/4
=>x=y
Đúng 3
Bình luận (0)
Giả sử x=\(\frac{a}{m}\),y=\(\frac{b}{m}\)( a,b,m thuộc Z , m > 0 ) và x< y . Hãy chứng tỏ rằng nếu chọn z = \(\frac{a+b}{2m}\)thì ta có x< z<y
Ta có x = \(\frac{2a}{2m}\)< \(\frac{a+b}{2m}\)= z
y = \(\frac{2b}{2m}\)> \(\frac{a+b}{2m}\)= z
Đúng 0
Bình luận (0)
Do x < y => a/m < b/m
=> a/m + a/m < a/m + b/m < b/m + b/m
=> 2x < a+b/m < 2y
=> x < a+b/m : 2 < 2y
=> x < a+b/m . 1/2 < y
=> x < a+b/2m < y
Chứng tỏ ...
Đúng 0
Bình luận (0)
có x<y\(\rightarrow\)\(\frac{a}{m}\)<\(\frac{b}{m}\)\(\rightarrow\)a<b
vì a<b \(\Rightarrow\)a+a<a+b suy ra 2a<a+b (1)
vì a<b\(\Rightarrow\)a+b<b+b suy ra a+b<2b
từ (1)(2) suy ra 2a <a+b <2b
\(\Rightarrow\)\(\frac{2a}{2m}\)<\(\frac{a+b}{2m}\)<\(\frac{2b}{2m}\)\(\rightarrow\)\(\frac{a}{m}\)<\(\frac{a+b}{2m}\)<\(\frac{b}{m}\)
\(\Rightarrow\)x<z<y
( nhớ cho mình tích đấy nha!)
,
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giả sử \(x=\frac{a}{m},y=\frac{b}{m}\left(a,b,m\varepsilon Z,m>0\right),x< y.\)Hãy chứng tỏ rằng nếu chọn \(Z=\frac{2a+1}{2m}\)thì ta có x<y<z
Vì x<y nên a<b. Ta có \(x=\frac{a}{m}=\frac{2a}{2m},y=\frac{b}{m}=\frac{2b}{2m}\)
Chọn \(z=\frac{2a+1}{2m}\).Do 2a<2a+1 nên x<z(1)
Do a<b nên a+1 < b suy ra 2a+1< 2b
TA có 2a+1< 2a+2< 2b nên 2a+1<2b do đó z<y(2)
Từ (1),(2) suy ra x<z<y
Ta có: x<y => \(\frac{a}{m}< \frac{b}{m}\)<=> a<b
Lại có:\(x=\frac{a}{m}=\frac{2a}{2m};y=\frac{b}{m}=\frac{2b}{2m}\)
vì a<b (a, b thuộc Z) <=> a+1 =< b hay 2a+2 =< 2b
=> 2a <2a+1<2a+2=<2b hay 2a<2a+1<2b
do đó: \(\frac{2a}{2m}< \frac{2+1}{2m}< \frac{2b}{2m}\)
=> x<y<z
Nguồn: loigiaihay.com