Vẽ tam giác ABC vuông tại B, vẽ tia phần giác C. C/m CM<\(\frac{AC+BC}{2}\)
TT
Những câu hỏi liên quan
Tam giác ABC, CM là tia phân giác của góc C, M thuộc AB. Vẽ AD vuông góc với CM, D thuộc CM. Cx là tia phân giác của góc ngoài tại C của tam giác ABC. Vẽ AE vuông góc với Cx, E thuộc Cx, DE căt AB, AC thứ tự tại P và Q. Tính tỉ số diện tích tam giác APQ và diện tích tam giác ABC
Cho tam giác ABC có AB = 6 cm;BC = 10 cm;AC=8 cm
a, chứng tỏ tam giác ABC vuông tại A
b, Vẽ phân giác BM của góc B (M thuộc AC) từ M Vẽ MN vuông BC (Nthuộc BC).Chứng minh rằng MA=MN
c,Tia NM cắt tia BA tại P.Chứng minh tam giác AMP =tam giác NMC rồi suy ra MP > MN
Hình tự vẽ
a) ΔABC vuông tại A.
Ta có: AB2 + BC2 = 62 + 82 = 100 (cm)
BC2 = 102 = 100 (cm)
Vì AB2 + BC2 = BC2 ( = 100 cm)
Nên ΔABC vuông tại A.
b) MA = MN.
Xét hai tam giác vuông ABM và NBM có:
BM: cạnh chung
∠ABM = ∠NBM (BM là phân giác của ∠ABC)
Do đó:ΔABM = ΔNBM (cạnh huyền - góc nhọn)
⇒ MA = MN (hai cạnh tương ứng)
c) ΔAMP = ΔNMC. MP > MN.
Xét hai tam giác vuông AMP và NMC có:
AM = MN (câu b)
∠AMP = ∠NMC (hai góc đối đỉnh)
Do đó: ΔAMP = ΔNMC (cạnh góc vuông - góc nhọn kề)
⇒ PM = MC (hai cạnh tương ứng) (1)
Xét ΔNMC vuông tại N có: MC > MN (định lí) (2)
Từ (1) và (2) suy ra: MP > MN
Đúng 0
Bình luận (0)
C5: Cho tam giác ABC vuông tại A biết AB = 15cm, AC = 20cm. Kẻ AH vuông góc BC tại H
a) CM: tam giác HBA đồng dạng tam giác ABC
b) Vẽ tia phân giác của góc BAH cắt BH tại D
c) Trên HC lấy điểm E sao cho HE = HA qua E vẽ đường thẳng vuông góc với BC và cắt AC tại M và qua C vẽ đường thẳng vuông góc với BC cắt theo phân giác của góc MEC tại F. CM: 3 điểm H ,M,F thẳng hàng
Xem chi tiết
a) Xét tam giác BHA và tam giác BAC có
góc BHA= góc BAC (=90)
góc B chung
=> tam giác BHA đồng dạng tam giác BAC (g.g)
Cho tam giác ABC cân tại A (góc A 90°). Vẽ AH vuông góc BC tại HA) cm rằng : tam giác ABH tam giác ACH rồi suy ra AH là tia phân giác góc AB) từ H vẽ HE vuông góc AB tại E, HF vuông góc AC tại F .Cm rằng tam giác EAH tam giác FAH rồi suy ra tam giác HEF là tam giác cân .C) Đường thẳng vuông góc với AC tại C cắt tia AH tại K. Cm rằng EH // BKD) Qua A vẽ đường thẳng song song với BC cắt tia HF tại N. Trên tia HE lấy điểm M sao cho HM HN. Chứng minh rằng M,A,N thẳng hàng
Đọc tiếp
Cho tam giác ABC cân tại A (góc A < 90°). Vẽ AH vuông góc BC tại H
A) cm rằng : tam giác ABH = tam giác ACH rồi suy ra AH là tia phân giác góc A
B) từ H vẽ HE vuông góc AB tại E, HF vuông góc AC tại F .Cm rằng tam giác EAH = tam giác FAH rồi suy ra tam giác HEF là tam giác cân .
C) Đường thẳng vuông góc với AC tại C cắt tia AH tại K. Cm rằng EH // BK
D) Qua A vẽ đường thẳng song song với BC cắt tia HF tại N. Trên tia HE lấy điểm M sao cho HM =HN. Chứng minh rằng M,A,N thẳng hàng
bạn sửa ý a b 2 tam giác bằng nhau theo trường hợp cạnh huyền góc nhọn
Đúng 0
Bình luận (0)
Cho tam giác ABC. Vẽ tia phân giác góc B; C cắt nhau tại O.Từ A vẽ đường thẳng vuông góc OA cắt các tia BO;CO lần lượt tại M;N.Chứng minh rằng BM vuông góc BN và CM vuông góc CN
Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo tại link trên nhé!
Đúng 0
Bình luận (0)
cho tam giác abc có ab=ac (ab< bc) gọi m là trung điểm của đoạn thẳng bc a cm tam giác abm =tam giác acm b vẽ me vuông góc với ab tại e, vẽ mf vuông góc với ac tại f cm ae= af c trên tia đối của tia fm lấy điểm d sao cho fd =fm cm góc dac= góc bam d cm tam giác adc là tam giác vuông
Xem chi tiết
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔAMF vuông tại F và ΔADF vuông tại F có
AF chung
MF=DF
Do đó: ΔAMF=ΔADF
=>góc MAF=góc DAF
=>góc DAF=góc BAM
Đúng 0
Bình luận (0)
Cho ABC có AB = 6 cm; AC = 8 cm; BC = 10 cm.
a) Chứng tỏ tam giác ABC vuông tại A.
b)Vẽ phân giác BM của góc B
( M thuộc AC), từ M vẽ MN BC ( N thuoocj BC).
Chứng minh MA = MN
c) Tia NM cắt tia BA tại P. Chứng minh tam giác AMP = tam giác NMC rồi suy ra MP > MN
Đang cần gấp...ko cần vẽ hình ... Vẽ thì càng tốt

a.
Xét \(\Delta ABC\) có:
\(AB^2+AC^2=6^2+8^2=100=10^2\)
Theo định lý Pythagoras đảo thì \(\Delta ABC\) vuông tại A
b.
Xét \(\Delta ABM\) và \(\Delta NBM\) có:
\(\widehat{ABM}=\widehat{NBM}\)
BM là cạnh chung
\(\widehat{BAM}=\widehat{BNM}=90^0\)
\(\Rightarrow\Delta ABM=\Delta NBM\left(ch-gn\right)\Rightarrow MA=MN\)
c.
Xét \(\Delta PAM\) và \(\Delta CNM\) có:
\(MA=MN\)
\(\widehat{PAM}=\widehat{MNC}\)
\(\widehat{AMP}=\widehat{CMN}\)
\(\Rightarrow\Delta PAM=\Delta CNM\left(g.c.g\right)\Rightarrow MN=MP\)
Do \(\Delta MNC\) vuông tại N nên \(MC>MN\left(ch>cgv\right)\)
\(\Rightarrow MP>MN\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB =5 cm ; AC = 12 cm ; BC = 13 cm :
a) C/m tam giác ABC vuông
b) trên cạnh BC , lấy điểm D sao cho BD = BA . Tia phân giác của góc B cắt cạnh AC ở điểm E. C/m AE = DE.
c) qua C , vẽ đường thẳng vuông góc với BE tại H , CH cắt đường thẳng AB tại F. C/m Tam giác BHF và Tam giác BHC.
d) C/m tam giác BAC = tam giác BDF.
e) C/m 3 điểm D , E , F thẳng hàng
Xem chi tiết
a) Ta có: \(BC^2=13^2=169\)
\(AB^2+AC^2=5^2+12^2=169\)
Do đó: \(BC^2=AB^2+AC^2\)(=169)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Đúng 0
Bình luận (0)
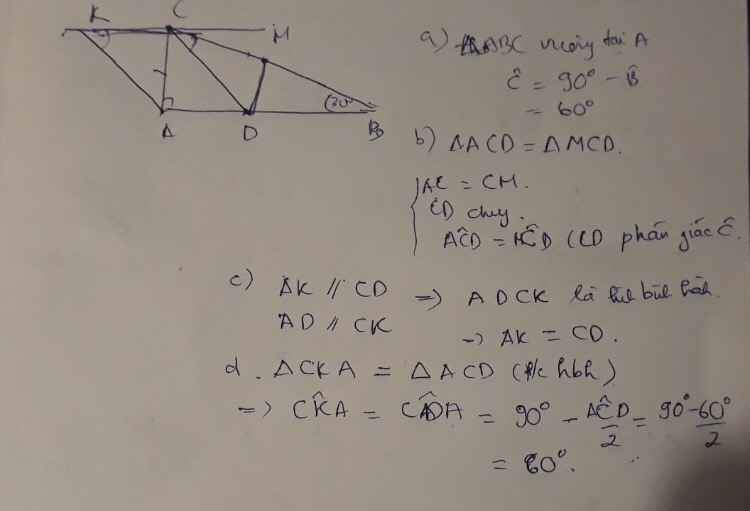
cho tam giác ABC vuông tại A có góc B=30⁰
a) tính góc C
b) vẽ tia phân giác của góc cắt cạnh AB tại D
c) Trên cạnh CB lấy điểm M sao cho CM=CA. CM tam giác ACD = tam giác MCD
d) Qua C vẽ đường thẳng xy vuông góc với CA. Từ A kẻ đường thẳng song song với CD cắt xy ở K. CM: AK=CD
e) tính góc AKC