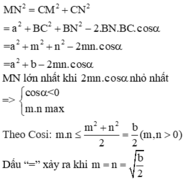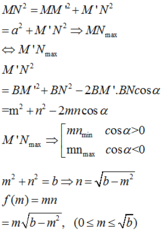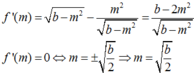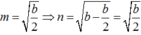nếu a,b>0 ta luôn có \(\frac{a+b}{2}\)>ab .hãy cho a,b 1 vài giá trị để thử lại
NA
Những câu hỏi liên quan
a, Tìm giá trị nguyên của x để biểu thức A frac{^{x^2+4}}{x-1}( với x khác 1) có giá trị là 1 số nguyên b, Cho các số a,b,c khác 0 thỏa mãn: a+b+c 0 và biểu thức: Pfrac{ab}{a^2+b^2-c^2}+frac{bc}{b^2+c^2-a^2}+frac{ca}{c^2+a^2-b^2}Chứng minh rằng: Giá trị của P khi được xác định luôn là một số hữu tỉ
Đọc tiếp
a, Tìm giá trị nguyên của x để biểu thức A = \(\frac{^{x^2+4}}{x-1}\)( với x khác 1) có giá trị là 1 số nguyên
b, Cho các số a,b,c khác 0 thỏa mãn: a+b+c = 0 và biểu thức:
P=\(\frac{ab}{a^2+b^2-c^2}\)+\(\frac{bc}{b^2+c^2-a^2}\)+\(\frac{ca}{c^2+a^2-b^2}\)
Chứng minh rằng: Giá trị của P khi được xác định luôn là một số hữu tỉ
Cho 2 biểu thức: \(A=\dfrac{5}{2m+1}\) và \(B=\dfrac{4}{2m-1}\)
Hãy tìm các giá trị của m để hai biểu thức ấy có giá trị thỏa mãn hệ thức:
a, 2A+3B=0 b, AB= A+B
Giải
a, 2A+3B=0 <=> \(\dfrac{10}{2m+1}+\dfrac{12}{2m-1}=0\)
<=>10(2m-1)+ 12(2m+1) =0
<=> 44m +2 =0
<=> m=-1/22
b, AB= A+B <=> \(\dfrac{20}{\left(2m-1\right)\left(2m+1\right)}=\dfrac{5}{2m+1}+\dfrac{4}{2m-1}\)
<=> 20 = 5(2m -1) + 4(2m+1)
<=> 20 = 18m - 1
<=> m=7/6
Đúng 0
Bình luận (0)
Chứng minh rằng nếu a,b>0 ta luôn có: \(\frac{a+2\sqrt{ab}+9b}{\sqrt{a}+3\sqrt{b}-2\sqrt[4]{ab}}-2\sqrt{b}=\left(\sqrt[4]{a}+\sqrt[4]{b}\right)^2\)
cho 2 biểu thức A=5/2m+1 và B=4/2m-1. hãy tìm giá trị m để a)2A+3B=0 b)AB=A+B
AB là đoạn vuông góc chung của 2 đường thẳng
∆
,
∆
chéo nhau,
A
∈
∆
,
B
∈
∆
,
A
B
a
;
M
là điểm di động trên
∆
,
N
là điểm di động trên
∆
. Đặt
A
M
m
,
...
Đọc tiếp
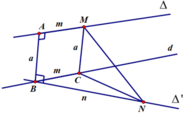
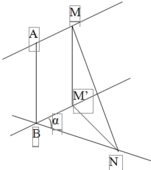
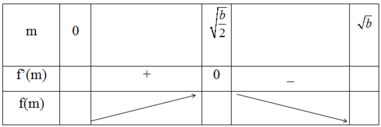
AB là đoạn vuông góc chung của 2 đường thẳng ∆ , ∆ ' chéo nhau, A ∈ ∆ , B ∈ ∆ ' , A B = a ; M là điểm di động trên ∆ , N là điểm di động trên ∆ ' . Đặt A M = m , A N = n m ≥ 0 , n ≥ 0 . Giả sử ta luôn có m 2 + n 2 = b với b > 0 không đổi. Xác định m, n để độ dài đoạn MN đạt giá trị lớn nhất.
A. m = n = a b 2
B. m = n = b 2
C. m = a 2 ; n = b 2
D. m = a b 2 ; n = a + b 2
Chứng minh rằng nếu a,b>0 thì ta luôn có
\(\frac{a+2\sqrt{ab}+9b}{\sqrt{a}+3\sqrt{b}-2\sqrt[4]{ab}}-2\sqrt{b}=\left(\sqrt[4]{a}+\sqrt[4]{b}\right)^2\)
AB là đoạn vuông góc chung của 2 đường thẳng
∆
,
∆
chéo nhau,
A
∈
∆
;
B
∈
∆
, AB a. M là điểm di động trên
∆
N là điểm di động trên
∆
. Đặt
A
M
m
;
A
N
n
(
m
≥...
Đọc tiếp
AB là đoạn vuông góc chung của 2 đường thẳng ∆ , ∆ ' chéo nhau, A ∈ ∆ ; B ∈ ∆ ' , AB= a. M là điểm di động trên ∆ N là điểm di động trên ∆ ' . Đặt A M = m ; A N = n ( m ≥ 0 ; n ⩾ 0 ) Giả sử ta luôn có m 2 + n 2 = b với b>0; b không đổi. Xác định m, n để độ dài đoạn MN đạt giá trị lớn nhất.
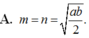
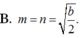
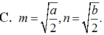
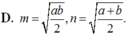
Các bạn giúp mình giải các bài toán này với:Cho hai số x và y thỏa mãn: x^2-y+frac{1}{4}0 và y^2-x+frac{1}{4}0. Tìm x và yCho ba số a,b,c thỏa: a+b+c0.Hãy tính giá trị của biểu thức:Pa2(a+3b)+b2(3b+b)+a(a+c)-b(b+c)+c3Chứng minh rằng biểu thức sau luôn có giá trị dương với mọi giá trị của biến:A(x+1)(x+3)(x+4)(x+6)+10Cảm ơn các bạn nhiều.
Đọc tiếp
Các bạn giúp mình giải các bài toán này với:
Cho hai số x và y thỏa mãn:
\(x^2-y+\frac{1}{4}=0\) và \(y^2-x+\frac{1}{4}=0\). Tìm x và y
Cho ba số a,b,c thỏa: a+b+c=0.Hãy tính giá trị của biểu thức:
P=a2(a+3b)+b2(3b+b)+a(a+c)-b(b+c)+c3
Chứng minh rằng biểu thức sau luôn có giá trị dương với mọi giá trị của biến:
A=(x+1)(x+3)(x+4)(x+6)+10
Cảm ơn các bạn nhiều.
Ta có: \(x^2-y+\frac{1}{4}=y^2-x+\frac{1}{4}=0\)
\(\Rightarrow\left(x^2-x+\frac{1}{4}\right)+\left(y^2-y+\frac{1}{4}\right)=0\)
\(\Rightarrow\left(x-\frac{1}{2}\right)^2+\left(y-\frac{1}{2}\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}x-\frac{1}{2}=0\\y-\frac{1}{2}=0\end{cases}\Rightarrow}x=y=\frac{1}{2}\)
Vậy \(x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
CMR nếu a; b >0 thì ta luôn có
\(\frac{a+2\sqrt{ab}+9b}{\sqrt{a}+3\sqrt{b}-2\cdot\sqrt[4]{ab}}\)\(-2\sqrt{b}=\left(\sqrt[4]{a}+\sqrt[4]{b}\right)^2\)