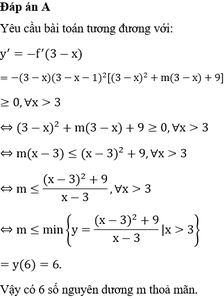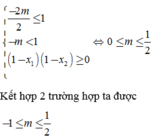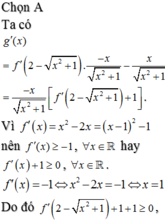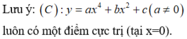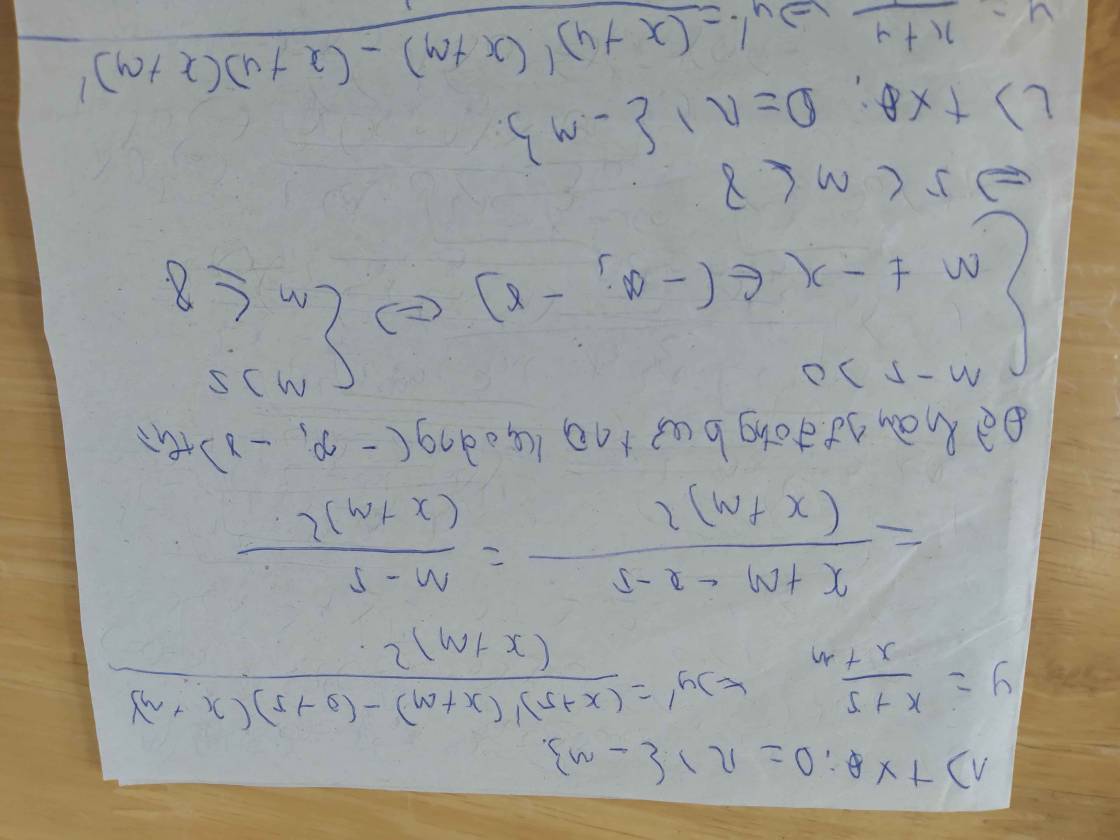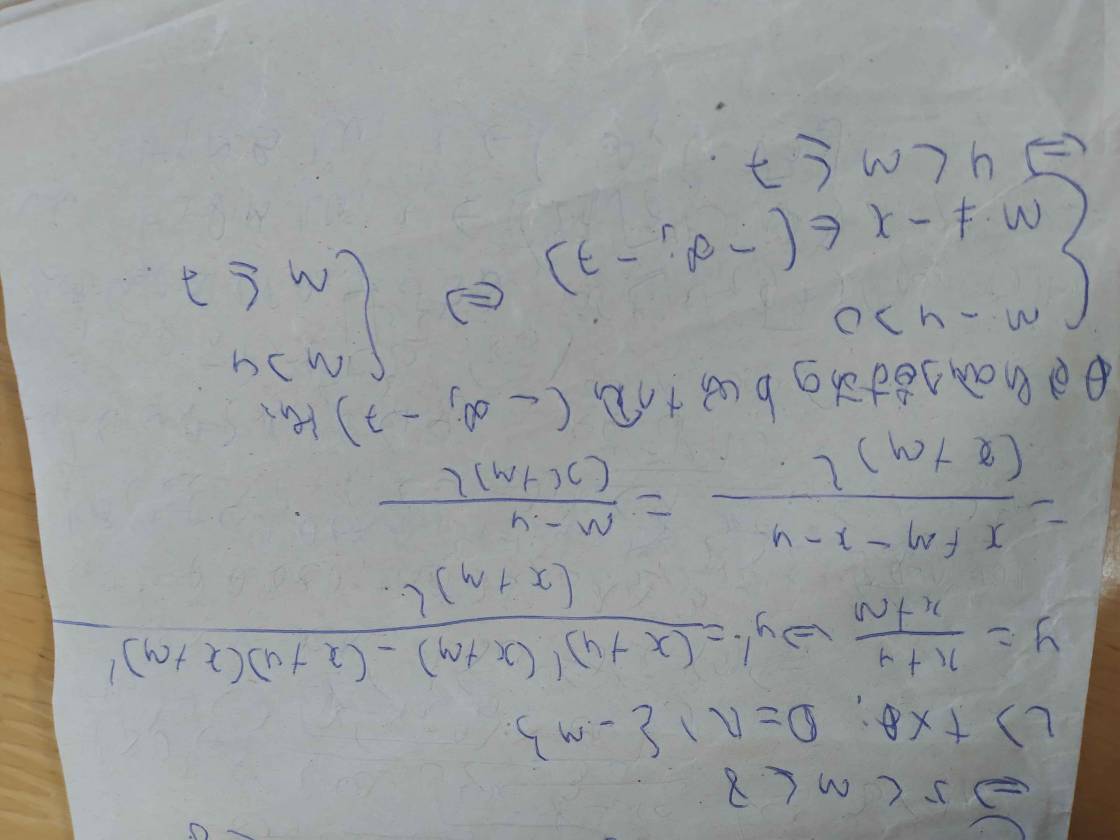hàm số y = x2 +(m+1)x +3 đồng biến trên (1;\(+\infty\) ) khi giá trị m thõa........
PT
Những câu hỏi liên quan
Với giá trị nào của m thì hàm số:
a) y = f(x) = (m-1)x +m2 -3 đồng biến trên R
b) y = f (x) = -x2 + (m-1)x+2 nghịch biến trên (1;2)
Tìm m để hàm số y đồng biến trên R
a, y = mx - x2 - 2x + mx2 + m
b, (m2 - 3m +2).x2 + (m - 1).x + \(\sqrt{3}\)
Lời giải:
a. $y=mx-x^2-2x+mx^2+m=x^2(m-1)+x(m-2)+m$
Lấy $x_1,x_2\in R$ sao cho $x_1\neq x_2$
$y(x_1)=x_1^2(m-1)+x_1(m-2)+m$
$y(x_2)=x_2^2(m-1)+x_2(m-2)+m$
Để hàm đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{x_1^2(m-1)+x_1(m-2)+m-[x_2^2(m-1)+x_2(m-2)+m]}{x_1-x_2}>0$
$\Leftrightarrow \frac{(m-1)(x_1^2-x_2^2)+(m-2)(x_1-x_2)}{x_1-x_2}>0$
$\Leftrightarrow (m-1)(x_1+x_2)+(m-2)>0$
Với mọi $x_1,x_2\in\mathbb{R}$ thì không có cơ sở để tìm $m$ sao cho hàm đồng biến.
b.
Xét tương tự câu 1, với $x_1\neq x_2\in \mathbb{R}$ thì hàm đồng biến khi:
$(m^2-3m+2)(x_1+x_2)+(m-1)>0$
Với mọi $x_1, x_2\in\mathbb{R}$ thì điều này xảy ra khi:
$m^2-3m+2=0$ và $m-1>0$
$\Leftrightarrow (m-1)(m-2)=0$ và $m-1>0$
$\Leftrightarrow m=2$
Đúng 2
Bình luận (0)
Cho hàm số yf(x) có đạo hàm f(x)
x
(
x
-
1
)
2
(
x
2
+
m
x
+
9
)
. Có bao nhiêu số nguyên dương m để hàm số yf(3-x) đồng biến trên khoảng
(
3
;
+
∞
)
. A. 6. B. 8. C. 5. D. 7.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Tìm m để hàm số
y
x
2
−
4
2
x
+
m
đồng biến trên đồng biến trên
1
;
+
∞
. A.
m
∈
−
4...
Đọc tiếp
Tìm m để hàm số y = x 2 − 4 2 x + m đồng biến trên đồng biến trên 1 ; + ∞ .
A. m ∈ − 4 ; 1 2 \ 0
B. m ∈ − 4 ; 1 2
C. m ∈ 0 ; 1 2
D. m ∈ − 1 2 ; 1 2
Cho hàm số
y
f
(
x
)
có đạo hàm
f
(
x
)
x
2
-
2
x
với mọi
x
∈
R
. Hàm số
g
(
x
)
f
2
-
x
2
+
1
-
x
2
+...
Đọc tiếp
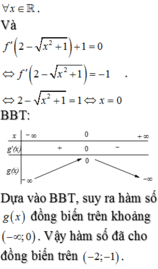
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x 2 - 2 x với mọi x ∈ R . Hàm số g ( x ) = f 2 - x 2 + 1 - x 2 + 1 - 3 đồng biến trên các khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị tham số m để hàm số
y
-
1
3
x
3
+
(
m
-
1
)
x
2
+
(
m
+
3
)
x
-
4
đồng biến trên (0;3) A.
m
≥
1
7
B.
m
≥
4
7...
Đọc tiếp
Tìm tất cả các giá trị tham số m để hàm số y = - 1 3 x 3 + ( m - 1 ) x 2 + ( m + 3 ) x - 4 đồng biến trên (0;3)
A. m ≥ 1 7
B. m ≥ 4 7
C. m ≥ 8 7
D. m ≥ 12 7
Tìm m để hàm số
y
2
x
4
-
(
3
-
m
)
x
2
+
1
đồng biến trên
-
∞
;
+
∞
Đọc tiếp
Tìm m để hàm số y = 2 x 4 - ( 3 - m ) x 2 + 1 đồng biến trên - ∞ ; + ∞
![]()
![]()
![]()
![]()
Cho hàm số
y
x
3
–
x
2
+
(
m
-
1
)
x
+
m
.
Tìm điều kiện của tham số m để hàm số đồng biến trên R A. m ≤ 2 B. m 2 C. m ≥ 2 D. m 2
Đọc tiếp
Cho hàm số y = x 3 – x 2 + ( m - 1 ) x + m . Tìm điều kiện của tham số m để hàm số đồng biến trên R
A. m ≤ 2
B. m > 2
C. m ≥ 2
D. m <2
Chọn B
y ' = x 2 - 2 x + ( m - 1 ) .
Hàm số đồng biến trên R ⇔ y' ≥ 0 ∀x ∈ R
⇒ Δ = ( - 1 ) 2 - ( m - 1 ) = - m + 2 ≤ 0 ⇔ m > 2
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số mđể hàm số
y
1
3
x
3
+
(
m
-
1
)
x
2
+
(
2
m
-
3
)
x
-
2
3
đồng biến trên
(
1
;
+
∞
)
A.
m...
Đọc tiếp
Tìm tất cả các giá trị của tham số mđể hàm số y = 1 3 x 3 + ( m - 1 ) x 2 + ( 2 m - 3 ) x - 2 3 đồng biến trên ( 1 ; + ∞ )
A. m > 2
B. m ≤ 2
D. m < 1
D. m ≥ 1
1) hàm số \(y=\dfrac{x+5}{x+m}\) đồng biến trên khoảng (\(-\infty\),-8)
2) hàm số \(y=\dfrac{x+4}{x+m}\) đồng biến trên khoảng (\(-\infty\),-7)
3) hàm số \(y=\dfrac{x+2}{x+m}\) đồng biến trên khoảng (\(-\infty\),-5)