\(x^4-y^4=\left(x^2\right)^2-\left(y^2\right)^2=\left(x^2+y^2\right)\left(x^2-y^2\right)=\left(x^2+y^2\right)\left(x+y\right)\left(x-y\right)\)

Bài 2: 

a: \(x^2+5x-6=\left(x+6\right)\left(x-1\right)\)

b: \(5x^2+5xy-x-y\)

\(=5x\left(x+y\right)-\left(x+y\right)\)

\(=\left(x+y\right)\left(5x-1\right)\)

c:\(-6x^2+7x-2\)

\(=-6x^2+3x+4x-2\)

\(=-3x\left(2x-1\right)+2\left(2x-1\right)\)

\(=\left(2x-1\right)\left(-3x+2\right)\)

1.

a) \(=x^2\left(x^2+2x+1\right)=x^2\left(x+1\right)^2\)

b) \(=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\)

\(=\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)

c) \(=5\left[\left(x^2-2xy+y^2\right)-4z^2\right]=5\left[\left(x-y\right)^2-4z^2\right]\)

\(=5\left(x-y-2z\right)\left(x-y+2z\right)\)

2.

a) \(=x\left(x+2\right)+3\left(x+2\right)=\left(x+2\right)\left(x+3\right)\)

b) \(=5x\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(5x-1\right)\)

c) \(=-\left[3x\left(2x-1\right)-2\left(2x-1\right)\right]=-\left(2x-1\right)\left(3x-2\right)\)

3.

b) \(=2x\left(x-1\right)+5\left(x-1\right)=\left(x-1\right)\left(2x+5\right)\)

c) \(=-\left[5x\left(x-3\right)-1\left(x-3\right)\right]=-\left(x-3\right)\left(5x-1\right)\)

4.

a) \(\Rightarrow\left(x-1\right)\left(5x-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\)

b) \(\Rightarrow2\left(x+5\right)-x\left(x+5\right)=0\)

\(\Rightarrow\left(x+5\right)\left(2-x\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)

Ta có : \(x^4-5x^2+4\)

\(=x^4-x^2-4x^2+4\)

\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)

\(=\left(x^2-1\right)\left(x^2-4\right)\)

\(=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)

Ta có: \(x^4-5x^2+4\)

\(=x^4-x^2-4x^2+4\)

\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)

\(=\left(x^2-1\right)\left(x^2-4\right)\)

\(=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)

x 4 - 5 x 2 + 4 = x 4 - 4 x 2 - x 2 + 4 = x 4 - 4 x 2 - x 2 - 4 = x 2 x 2 - 4 - x 2 - 4 = x 2 - 4 x 2 - 1 = x + 2 x - 2 x + 1 x - 1

Ta có: 

Ta có:

| x 4   –   5 x 2   +   4 |

Đáp án D

Xét hàm y = x 4   –   5 x 2   +   4

⇒ y’ = 4x3 – 10x

⇒ y’ = 0 ó x = 0 hoặc x =  ± 5 2

Ta có bảng biến thiên

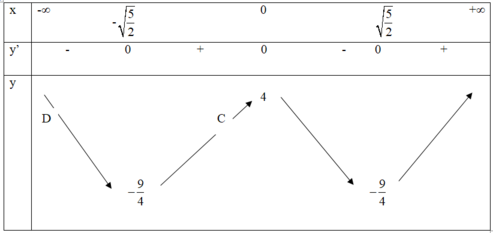
Ta có bảng biến thiên hàm y = | x 4   –   5 x 2   +   4 |

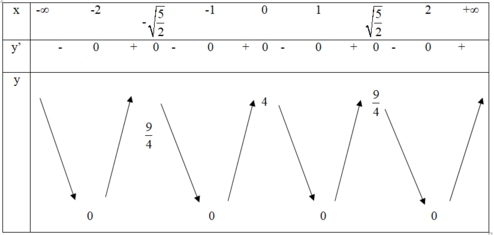
Vậy phương trình có 8 nghiệm ó đường y = m giao đồ thị hàm số y = | x 4   –   5 x 2   +   4 | tại 8 điểm phân biệt

⇔ 0 < m < 9 4

Đáp án D

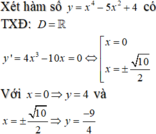
Bước 1: Ta giữ nguyên phần đồ thị phía trên trục hoành.

Bước 2: Lấy đối xứng phần phía dưới trục hoành của đồ thị lên phía trên trục hoành và xóa bỏ đi phần đồ thị nằm phía dưới trục hoành ta được đồ thị hàm số  y = x 4 - 5 x 2 + 4

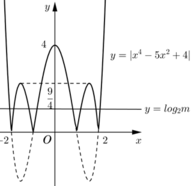
Khi đó số nghiệm của phương trình  x 4 - 5 x 2 + 4 = log 2 m chính là số giao điểm của đồ thị hàm số  y = x 4 - 5 x 2 + 4  và đường thẳng  y = log 2 m với m > 0.Dựa vào đồ thị hàm số  y = x 4 - 5 x 2 + 4  ta thấy để phương trình  x 4 - 5 x 2 + 4 = log 2 m  có 8 nghiệm thì:  0 < log 2 m < 9 4 ⇔ 1 < m < 2 9 4

\(\text{x^3 – 5x^2 + 8x – 4 }\)

\(\text{= x^3 – 4x^2 + 4x – x^2 + 4x – 4}\)

\(\text{= x( x^2 – 4x + 4 ) – ( x^2 – 4x + 4 )}\)

\(\text{= ( x – 1 ) ( x – 2 )^2}\)

\(x^3-5x^2+8x-4=x^3-x^2-4x^2+4x-4\\ =x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)\\ =\left(x^2-4x+4\right)\left(x-1\right)\\ =\left(x-2\right)^2\left(x-1\right)\)

Đáp án D