Cho đường tròn (O) đường kính AB. Kẻ 2 dây AC bà BD song song. Chứng minh: AC=BD
KT
Những câu hỏi liên quan
Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. Chứng minh AC = BD
Đường thẳng qua O và vuông góc với AC và BD lần lượt tại H và K (H ∈ AC; KBD)
Ta có ∆AOH = ∆BOK (g.c.g) => AK = BK => AC = BD
Đúng 0
Bình luận (0)
Cho đường tròn (O), đường kính AB. Kẻ hai dây song son AC và BD. Chứng minh rằng:
a) AC = BD;
b) Ba điểm C, O, D thẳng hàng.
a Tg aeo=tg bfo,bABCD la hinh binh hanh
Giải thích các bước giải:
a)Ta có :
Xét tam giác DOB và tam giác AOC , ta có :
(hai gócsole trong mà )
(hai góc đối đỉnh )
(cạnh tương ứng)
b) Ta có :
mà
Xem thêm câu trả lời
Cho (O) đường kính AB, kẻ hai dây AC và BD song song với nhau.
a) Chứng minh AC= BD; b) Chứng minh 3 điểm C, O, D thẳng hàng.
Cho đường tròn (O) có AB là đường kính. Vẽ hai dây AD và BC song song nhau. Chứng minh:
a, AC = BD
b, CD là đường kính của (O)
Cho đường tròn (O) đường kính AC và điểm B trên nửa đường tròn sao cho sđ cung BC =60°. Qua B kẻ dây BD vuông góc AC, qua D kẻ dây DF song song AC.
a, Tính số đo các cung CD, AB, FD
b, Tìm tiếp tuyến của (O) song song với AB
a: Xét (O) có
ΔBAC nội tiếp
AC là đường kính
Do đó: ΔBAC vuông tại B
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BC}=\dfrac{1}{2}\cdot60^0=30^0\)
Gọi H là giao điểm của BD với AC
BD\(\perp\)AC nên BD\(\perp\)AC tại H
ΔOBD cân tại O
mà OH là đường cao
nên H là trung điểm của BD
Xét ΔCBD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCBD cân tại C
=>CB=CD
Xét ΔCOD và ΔCOB có
CD=CB
OD=OB
CO chung
Do đó: ΔCOD=ΔCOB
=>\(\widehat{COD}=\widehat{COB}\)
=>\(sđ\stackrel\frown{CB}=sđ\stackrel\frown{CD}=60^0\)
Xét ΔBAC vuông tại B có \(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(\widehat{BCA}+30^0=90^0\)
=>\(\widehat{BCA}=60^0\)
Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{BCA}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}\)
=>\(sđ\stackrel\frown{AB}=2\cdot\widehat{BCA}=120^0\)
DF//AC
DB\(\perp\)AC
Do đó: DF\(\perp\)DB
=>ΔDFB vuông tại D
ΔDFB vuông tại D
nên ΔDFB nội tiếp đường tròn đường kính BF
mà ΔDFB nội tiếp (O)
nên O là trung điểm của BF
=>OA//DF
=>\(\widehat{BFD}=\widehat{BOH}=\widehat{BOC}\)(hai góc đồng vị)
=>\(\widehat{BFD}=60^0\)
ΔBDF vuông tại D
=>\(\widehat{BFD}+\widehat{FBD}=90^0\)
=>\(\widehat{FBD}+60^0=90^0\)
=>\(\widehat{FBD}=30^0\)
Xét (O) có
\(\widehat{FBD}\) là góc nội tiếp chắn cung FD
Do đó: \(\widehat{FBD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{FD}\)
=>\(sđ\stackrel\frown{FD}=2\cdot\widehat{FBD}=2\cdot\)30=60 độ
Đúng 1
Bình luận (0)
Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ dây CD song song với AB. Chứng minh rằng BC = BD.
Ta có OB ⊥ AB và AB // CD nên OB ⊥ CD. Gọi H là giao điểm của BO và CD thì BH ⊥ CD, suy ra HC = HD. Do đó BC = BD.
Đúng 1
Bình luận (0)
Cho đường tròn tâm O, đường kính AB, vẽ hai dây AB CD song song nhau. kẽ OI vuông góc AC a) Chứng minh OI vuông góc BD tại K. b ) Chứng minh tam giác IOA = tam giác OKB. c) So sánh AC và BD
Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ dây CD song song với AB. Chứng minh rằng BC = BD ?
Cho đường tròn (O) đường kính AB. Kẻ hai dây AC và BD song song. Chọn khẳng định đúng trong các khẳng định sau.
A. AC = BD
B.AC = 2 BD
C. BD = 2 AC
D. Tất cả sai
Đáp án A
Qua O dựng đường thẳng vuông góc với AC và BD. Đường thẳng này cắt AC và BD lần lượt tại M và N.
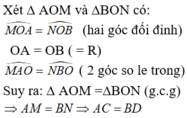
Đúng 0
Bình luận (0)




