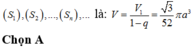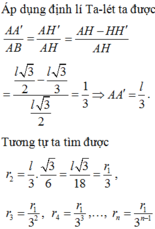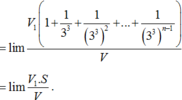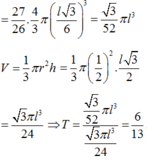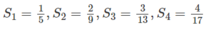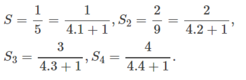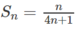Gọi Sn là tổng các số tự nhiên n. Tính tổng: S1+S2+S3+...+S2012+S2013
NN
Những câu hỏi liên quan
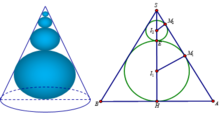
Cho hình nón (N) có góc ở đỉnh bằng 600 độ dài đường sinh bằng a. Dãy hình cầu (S1), (S2), (S3),… (Sn) thỏa mãn: (S1) tiếp xúc với mặt đáy và các đường sinh của hình nón (N) ; (S2) tiếp xúc ngoài với (S3) và tiếp xúc với các đường sinh của hình nón (N), (S3) tiếp xúc ngoài với (S2) và tiếp xúc với các đường sinh của hình nón (N). Tính tổng thể tích các khối cầu (S1), (S2), (S3),… (Sn) theo a.
Đọc tiếp
Cho hình nón (N) có góc ở đỉnh bằng 600 độ dài đường sinh bằng a. Dãy hình cầu (S1), (S2), (S3),… (Sn) thỏa mãn: (S1) tiếp xúc với mặt đáy và các đường sinh của hình nón (N) ; (S2) tiếp xúc ngoài với (S3) và tiếp xúc với các đường sinh của hình nón (N), (S3) tiếp xúc ngoài với (S2) và tiếp xúc với các đường sinh của hình nón (N). Tính tổng thể tích các khối cầu (S1), (S2), (S3),… (Sn) theo a.
![]()
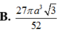
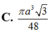

Cho hình vuông có cạnh là 1. Nối các trung điểm của hình vuông trên ta được một hình vuông có diện tích
S
1
tiếp tục quá trình trên với các hình vuông với diện tích là
S
1
;
S
3
;
.
.
.
;
S
n
;
.
.
.
Tính tổng vô hạn
S
1...
Đọc tiếp
Cho hình vuông có cạnh là 1. Nối các trung điểm của hình vuông trên ta được một hình vuông có diện tích S 1 tiếp tục quá trình trên với các hình vuông với diện tích là S 1 ; S 3 ; . . . ; S n ; . . . Tính tổng vô hạn S 1 + S 2 + S 3 + . . . + S n + . . .
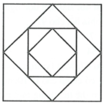
A. 1
B. 1/2
C. 2
D. 3/2
cho tổng
S
n
1
1
.
2
+
1
2
.
3
+
.
.
.
+
1
n
n
+...
Đọc tiếp
cho tổng S n = 1 1 . 2 + 1 2 . 3 + . . . + 1 n n + 1 với n ∈ N *
a.Tính S1, S2, S3
b.Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
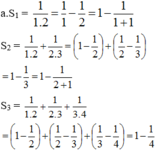
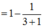
b. Dự đoán: 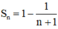
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
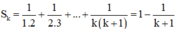
Khi đó:
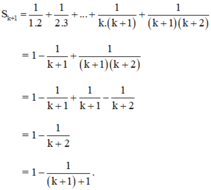
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*
Đúng 0
Bình luận (0)
Cho khối nón có độ lớn góc ở đỉnh là
π
3
. Một khối cầu
(
S
1
)
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3...
Đọc tiếp
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 1 ;..; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , . . . . . , V n - 1 , V n , lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , . . . . . , S n - 1 , S n , và V là thể tích của khối nón. Tính giá trị của biểu thức T = l i m V 1 + V 2 + . . . + V n V .
![]()
![]()
Cho tổng:
S
n
1
1
.
5
+
1
5
.
9
+
.
.
.
+
1
4
n
-...
Đọc tiếp
Cho tổng: S n = 1 1 . 5 + 1 5 . 9 + . . . + 1 4 n - 3 4 n + 1
a) Tính S 1 , S 2 , S 3 , S 4 ;
b) Dự đoán công thức tính S n và chứng minh bằng phương pháp quy nạp.
Cho khối nón có độ lớn góc ở đỉnh là
π
3
. Một khối cầu (
S
1
) nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3
là khối tiếp xúc với tất cả các đường sinh của nón với
S
2
;…;...
Đọc tiếp
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 2 ;…; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , … , V n - 1 , V n lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , … , S n và V là thể tích của khối nón. Tính giá trị của biểu thức T = lim n → + ∞ V 1 + V 2 + . . . + V n V
A. 3 5
B. 6 13
C. 7 9
D. 1 2
Chọn đáp án B
Thiết diện qua trục của hình nón là một tam giác đều cạnh l.
Do đó bán kính đường tròn nội tiếp tam giác cũng chính là bán kính mặt cầu nội tiếp chóp là
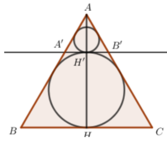
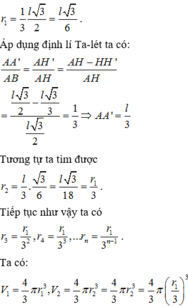

Đúng 0
Bình luận (0)
Cho khối nón có góc ở đỉnh của thiết diện qua trục là
π
3
. Một khối cầu
S
1
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
2
;...;
S...
Đọc tiếp
Cho khối nón có góc ở đỉnh của thiết diện qua trục là π 3 . Một khối cầu S 1 nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 2 ;...; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , ... V n − 1 , V n lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , ... , S n − 1 , S n và V là thể tích của khối nón. Tính giá trị biểu thức T = lim n → + ∞ V 1 + V 2 + ... + V n V
A. 7 9 .
B. 1 2 .
C. 6 13 .
D. 3 5 .
Cho khối nón có góc ở đỉnh của thiết diện qua trục là
π
3
. Một khối cầu (S1) nội tiếp trong khối nón. Gọi S2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S1; S3 là khối tiếp xúc với tất cả các đường sinh của nón và với S2; ….; Sn là khối cầu tiếp xúc với tất cả các đường sinh của nón và với Sn-1. Gọi V1, V2, V3, … , Vn-1, Vn lần lượt là thể tích của khối cầu S1, S2, S3, …, Sn-1, Sn và V là thể tích của khối nón. Tính giá trị biểu thức...
Đọc tiếp
Cho khối nón có góc ở đỉnh của thiết diện qua trục là π 3 . Một khối cầu (S1) nội tiếp trong khối nón. Gọi S2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S1; S3 là khối tiếp xúc với tất cả các đường sinh của nón và với S2; ….; Sn là khối cầu tiếp xúc với tất cả các đường sinh của nón và với Sn-1. Gọi V1, V2, V3, … , Vn-1, Vn lần lượt là thể tích của khối cầu S1, S2, S3, …, Sn-1, Sn và V là thể tích của khối nón. Tính giá trị biểu thức T = l i m n → + ∞ = V 1 + V 2 + . . . + V n V
![]()
![]()
![]()
![]()
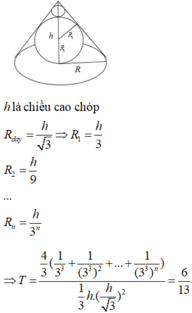
Đáp án C
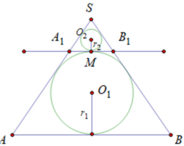
Ta dễ dàng nhìn thấy quy luật của thể tích các khối cầu
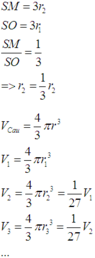
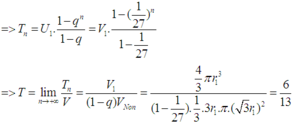
Đúng 0
Bình luận (0)
Cho khối nón có góc ở đỉnh của thiết diện qua trục là
π
3
. Một khối cầu
S
1
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3
là khối tiếp xúc với tất cả các đường sinh của nón và với...
Đọc tiếp
Cho khối nón có góc ở đỉnh của thiết diện qua trục là π 3 . Một khối cầu S 1 nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón và với S 2 ; . . . ; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , ... , V n − 1 , V n lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , ... , S n − 1 , S n và V là thể tích của khối nón. Tính giá trị biểu thức T = lim n → + ∞ V 1 + V 2 + ... + V n V .
A. 7 9
B. 1 2
C. 6 13
D. 3 5
Đáp án C
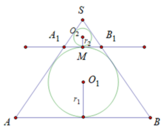
Ta dễ dàng nhìn thấy quy luật của thể tích các khối cầu
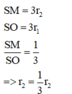
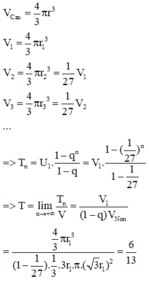
Đúng 0
Bình luận (0)