Cho tam giác ABC .vẽ đoạn thẳng AB sao cho AB=BC và đoạn thẳng AB song song BC
NT
Những câu hỏi liên quan
Cho tam giác ABC vẽ đoạn thẩng AD sao cho AD=BC và đoạn thẳng AB song song B
(giúp mình với mình cần gấp lắm)
Cho tam giác ABC có AB=AC, AM là tia phân giác của góc A (M thuộc BC)
a) chứng minh: tam giác ABC= tam giác ACM
b) Trên tia đối của tia MA lấy điểm D sao cho MD=MA.chứng minh AB song song với DC
c) Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ đoạn thẳng AE sao cho AE song song với BC và AE=BC. Chứng minh D,C,E thẳng hàng
cho tam giác abc vuông tại a .Ab =24cm.điểm d trên cạnh ac sao cho cd=2 lần ad.Qua d vẽ đường thẳng song song với ab cắt bc ở e.Tính độ dài đoạn thẳng de
Rồng bay ở Thăng Long đáp xuống Hạ Long
tui giai duoc ket ban voi tui nha
Xem thêm câu trả lời
Cho tam giác ABC Vẽ đoạn thẳng AD Sao cho AD=BC Và đoạn thẳng AD song song BC
Cho tam giác ABC. Qua điểm D thuộc cạnh AB vẽ đường thẳng song song với BC cắt AC ở E. Biết: DB=4cm,AB=6,8cm và AE=4,2cm.
Tính độ dài đoạn thẳng AD và EC
AD=6,8-4=2,8cm
DE//BC
=>AE/EC=AD/DB
=>4,2/EC=2,8/4=7/10
=>EC=6cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB 6cm,AC 8cm và BC 10cm. Lấy điểm B trên AB sao cho . Qua B vẽ đường thẳng song song với BC và cắt AC tại C.a) Tính AC.b) Qua C vẽ đường thẳng song song với AB và cắt BC tại D. Tính BD,BC.c) Tính và so sánh các tỉ số: frac{{AB}}{{AB}},frac{{AC}}{{AC}} và frac{{BC}}{{BC}}.
Đọc tiếp
Cho tam giác \(ABC\) có \(AB = 6cm,AC = 8cm\) và \(BC = 10cm\). Lấy điểm \(B'\) trên \(AB\) sao cho . Qua \(B'\) vẽ đường thẳng song song với \(BC\) và cắt \(AC\) tại \(C'\).
a) Tính \(AC'\).
b) Qua \(C'\) vẽ đường thẳng song song với \(AB\) và cắt \(BC\) tại \(D\). Tính \(BD,B'C'\).
c) Tính và so sánh các tỉ số: \(\frac{{AB'}}{{AB}},\frac{{AC'}}{{AC}}\) và \(\frac{{B'C'}}{{BC}}\).
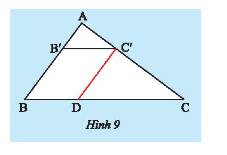
a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
Đúng 1
Bình luận (0)
Cho tam giác ABC. Điểm D thuộc cạnh BC. Ve DE song song voi AC( E thuộc AB), vẽ DF song song với AB. Trên đoạn thẳng DE lấy điểm K sao cho EK=CF, Chứng minh AK đi qua trung điểm của BC
cho hình tam giác abc vuông tại a,ab=18cm.diểm d trên cạnh ac và ad=1/3 ac.qua d vẽ đường thẳng song song với ab cắt bc ở e.tính độ dài đoạn thẳng de
cho tam giác ABC vuông tại A,AB=9cm; AC=12cm.Trên tia BC lấy D sao cho BD=BA.Kẻ đoạn thẳng D vuông với BC. Đoạn thẳng này cắt AC tại E, cắt AB tại K
a) tính BC?
b) cm tam giác ABE=tam giác DBE => BE là tia phân giác của góc ABC
c)AC song song DK
d)kẻ đoạn thẳng A vuông góc với BC tại H, đoạn thẳng này cắt BE tại M. CM tam giác AME cân


