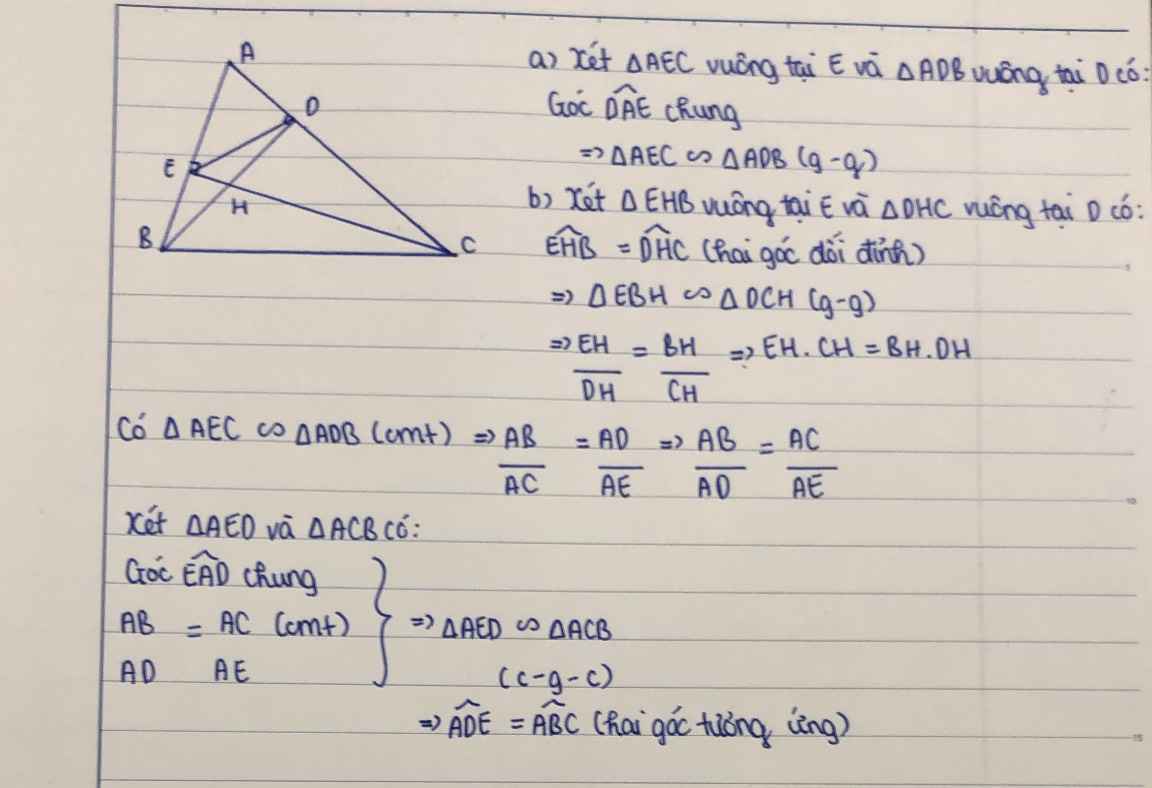Tam giác ADE và tg ABC có 

\(\hept{\begin{cases}\widehat{A}chung\\\\\frac{AD}{AE}=\frac{AB}{AC}\left(\frac{AD}{AB}=\cos\widehat{A}=\frac{AE}{AC}\right)\end{cases}}\)

Suy ra ADE đồng dạng ABC

=> đpcm

sorry mk ch hojccasi này

Không lẠm

mình làm được câu a, b, c rồi các bạn giúp mình câu d nhé thank

a) + ΔABD ∼ ΔACE ( g.g )

⇒ABAD=ACAE⇒ABAC=ADAE⇒ABAD=ACAE⇒ABAC=ADAE

b) + ΔBHE ∼ ΔCHD ( g.g )

⇒HBHE=HCHD⇒HBHE=HCHD

⇒HB⋅HD=HC⋅HE⇒HB⋅HD=HC⋅HE

c) + ΔADE ∼ ΔABC ( c.g.c )

⇒ADEˆ=ABCˆ

Tam giác ADE và tg ABC có 
góc A chung

AD/AE=AB/AC ( AD/AB=cos góc A =AE/AC)

suy tam giác ADE đong dang zs tam giác ABC

Gọi M là trung điểm của BC

Lúc đó thì EM, DM lần lượt là trung tuyến ứng với cạnh huyền của hai tam giác vuông BEC, BDC

\(\Rightarrow MB=ME=MC=MD\)

Do đó tam giác BEM; CMD và EDM cân tại M

Ta có: \(\widehat{ADE}=180^0-\widehat{MDE}-\widehat{MDC}\)

\(=180^0-\frac{180^0-\widehat{EMD}}{2}-\frac{180^0-\widehat{DMC}}{2}\)

\(=\frac{\widehat{EMD}+\widehat{DMC}}{2}=\frac{180^0-\widehat{EMB}}{2}=\frac{2\widehat{MBE}}{2}=\widehat{ABC}\)

Vậy \(\widehat{ADE}=\widehat{ABC}\left(đpcm\right)\)

AI bit chi dum di

vẽ hình

a xét tam giác ABD và tam giác ACE có :

chung góc BAC

góc BDA = góc CEA = 90 độ

=> tam giác ABD đồng dạng tam giác ACE (g.g)

b, xét tam giác EHB và tam giác DHC có

góc BDC = góc CFB = 90 độ 

góc BHF = góc DHC ( đối đỉnh )

=> tam giác EHB đồng dạng với tam giác DHC (g.g)

=> \(\frac{HB}{HC}=\frac{HE}{HD}\) 

=> HD . HB = HE . HC ( đpcm )

c, vì tam giác ABD đồng dạng với tam giác ACE ( câu a)

=> \(\frac{AB}{AC}=\frac{AD}{AE}\)  => \(\frac{AE}{AC}=\frac{AD}{AB}\)

xét tam giác ADE và tam giác ABC có 

chung góc BAC

\(\frac{AE}{AC}=\frac{AD}{AB}\) 

=> tam giác ADE đồng dạng với tam giác ABC ( c.g.c) 

=> góc ADE = góc ABC ( đpcm)

a, Xét Δ ABD và Δ ABE, có :

\(\widehat{ADB}=\widehat{AEB}=90^o\)

\(\widehat{BAD}=\widehat{BAE}\) (góc chung)

=> Δ ABD ∾ Δ ABE (g.g)

b, Xét Δ EHB và Δ DHC, có :

\(\widehat{EHB}=\widehat{DHC}\) (đối đỉnh)

\(\widehat{HEB}=\widehat{HDC}=90^o\)

=> Δ EHB ∾ Δ DHC (g.g)

=> \(\dfrac{EH}{DH}=\dfrac{HB}{HC}\)

=> \(HB.HD=HC.HE\)

CHÚC EM HỌC TỐT NHÉ

http://vchat.vn/pictures/service/2016/07/clo1468398982.PNG

copy trnag nay roi vao

suy ra góc ADE = góc ABC nhé

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có

góc A chung

=>ΔABD đồng dạng với ΔACE

b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC

=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC

=>góc ADE=góc ABC