Cho \(\Delta ABC\). Gọi \(M\) là trung điểm của đoạn thẳng \(BC\). Biết \(\widehat{BAM}=m^o\); \(\widehat{MAC}=n^o\).
a, Tính \(\widehat{BAC}\)
b, Với giá trị nào của \(m^o\) và \(n^o\) thì \(AM\) là tia phân giác của \(\widehat{BAC}\)?
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho \(\Delta ABC\) có H là trực tâm . Gọi P là 1 điểm thuộc đoạn thẳng AB , gọi Q là 1 điểm thuộc đoạn thẳng AC sao cho \(\widehat{BHP}=\widehat{CHQ}=90^0\) . Gọi M là trung điểm của đoạn thẳng BC. Chứng minh rằng HM vuông góc với PQ .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em với ạ, em cám ơn ạ!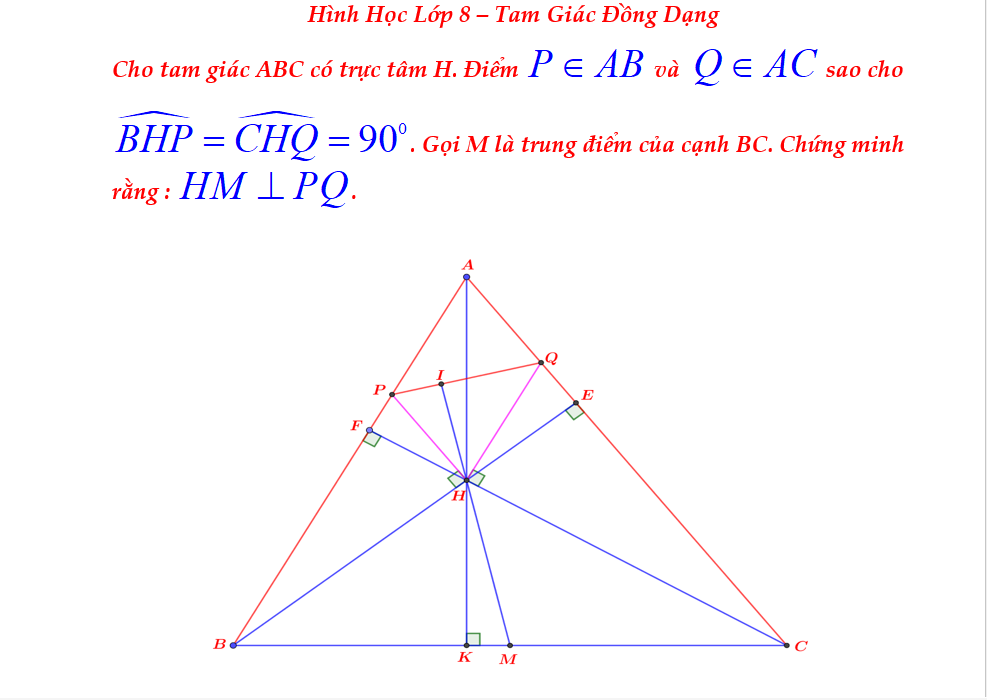
Qua C kẻ đường thẳng song với PQ, cắt AB tại N, cắt AH tại K
HP=HQ
=>KN=KC
=>KM là đường trung bình của ΔCBN
=>KM//NB
=>KM vuông góc CH
M là trực tâm của ΔCHK
=>HM vuông góc nC
=>HM vuông góc PQ
Cho tam giác ABC, gọi M là trung điểm của cạnh BC. Qua điểm A kẻ đường thẳng song song với BC và trên đường thẳng đó lấy D sao cho AD=AM(M và D nằm khác phía đối với AB)
a) Chứng minh \(\Delta\) ABD = \(\Delta\)BAM
b)Chứng minh AM // BD và AM=BD
c)Gọi I là trung điểm của đoạn thẳng AM.Chứng minh D,I,C thẳng hàng
d)Giả sử BD=BM.Chứng minh rằng \(\widehat{BAC}\) =\(^{90^o}\)
Bạn tự vẽ hình nha!!!
a.)Xét\(\Delta ABD\)và\(\Delta ABM\)có:
\(AD=BM\)
\(AB:\)Chung
\(\widehat{DAB}=\widehat{ABM}\left(slt\right)\)
\(\Rightarrow\Delta ABD=\Delta BAM\)
b.)Ta có:\(\Delta ABD=\Delta BAM\)(Theo a)
\(\Rightarrow\widehat{DBA}=\widehat{BAM}\)(mà 2 góc SLT)
\(\Rightarrow AM//BD\)
c.)Xét\(\Delta ADI\)và\(\Delta IMC\)có:
\(AD=CM\)
\(\widehat{DAI}=\widehat{IMC}\)
\(AI=IM\)
\(\Rightarrow\Delta AID=\Delta IMC\)
\(\Rightarrow IA=IC\)
\(\Rightarrow I\)là trung điểm của\(AC\)
\(\Rightarrow I,A,C\)thẳng hàng(đpcm)
P/s:#Study well#
Cho \(\Delta ABC\), M là trung điểm của BC, \(\widehat{BAM}=30^o,\widehat{MAC}=15^o\). Tính góc BCA
Cho \(\Delta ABC\)vuông cân tại A. Gọi M là trung điểm của BC, D là điểm thuộc đoạn BM (D khác B và M). Kẻ các đường thẳng BH, CI lần lượt vuông góc với đường thẳng AD tại H và I. Chứng minh rằng :
a) \(\widehat{BAM}=\widehat{ACM}\)và BH = AI
b) \(\Delta MHI\)vuông cân.
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
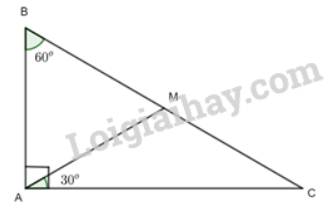
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.
1. Cho tam giác ABC cân tại B. Kẻ AM ⊥ BC (M ∈ BC) và CN ⊥ BA (N ∈ BA):
a) Chứng minh rằng: ΔBAM = ΔBCN.
b) Gọi O là giao điểm của AM và CN.
Chứng minh rằng: ΔNOA = ΔMOC
c) Chứng minh rằng: BO là phân giác của \(\widehat{ABC}\) .
d) Lấy điểm H sao cho AC là trung trực của đoạn thẳng OH. Tìm điều kiện của ΔABC để ΔOCH đều.
Chi can lam cau d la duoc
Cho tam giác ABC
a) giả sử \(\widehat{A}=60^o,\widehat{B}=70^o\).Tính số đo góc \(\widehat{C}\)
b) Gọi M là trung điểm của AB.Vẽ MD // BC, cắt AC tại D. TRên tia BC lấy điểm E sao cho BE = MD. Chứng minh \(\Delta AMD=\Delta MBE\)
c) Chứng minh ME // AC
d) Gọi I là trung điểm của DE. Chứng minh ba điểm M,I,C thẳng hàng
Cho \(\Delta ABC\)vuông cân tại A. Gọi M là trung điểm của BC, D là điểm thuộc đoạn BM (D khác B và M). Kẻ các đường thẳng BH, CI lần lượt vuông góc với đường thẳng AD tại H và I. Chứng minh rằng :
a) \(\widehat{BAM}=\widehat{ACM}\)và BH = AI
b) \(\Delta MHI\)vuông cân.
a) Bạn nối điểm A với M trên hình vẽ giúp mình nhé, mình quên chưa vẽ...
Xét \(\Delta ABM,\Delta ACM\) có :
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{ABM}=\widehat{ACM}\left(gt\right)\\BM=MC\left(\text{M là trung điểm của BC}\right)\end{matrix}\right.\)
=> \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
=> \(\widehat{BAM}=\widehat{ACM}\) ( 2 góc tương ứng)
Xét \(\Delta ABH,\Delta CAI\) có :
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{AHB}=\widehat{CIA}=90^o\\\widehat{BAH}=\widehat{ACI}\left(=90^o-\widehat{IAC}\right)\end{matrix}\right.\)
=> \(\Delta ABH=\Delta CAI\left(ch-gn\right)\)
=> BH = AI (2 cạnh tương ứng)
Cho tam giác ABC cân tại A, gọi M là trung điểm của canh BC. Trên đoạn thẳng MB lấy điểm D, trên đoạn thẳng MC lấy điểm E sao cho BD=CE. Kẻ \(DH\perp AB,EK\perp AC\left(H\in AB,K\in AC\right)\).Gọi O là giao điểm của DH và EK. Chứng minh
a) \(\Delta ABD=\Delta ACE\)
b) DH=EK
c) AO là phân giác của \(\widehat{BAC}\)
d) 3 điểm A,M,O thẳng hàng