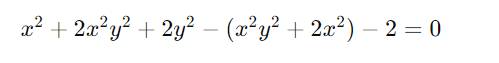2x² + 2y² = 5xy

=> 2x² + 2y² - 5xy = 0

=> (x - 2y)(2x - y)   = 0 

x = 2y (loại)

y = 2x

E = \(\dfrac{x+2x}{x-2x}\)=-3

Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)

Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)

Chứng minh tương tự:

\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)

Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)

Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\) 

Bạn tham khảo nhé

https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737

-2\(x^2+xy^2\)        (\(xy^2\) là \(1xy^2\) )        

=(\(-2+1\))  (\(x^2.x\)) . \(y^2\)          (Ta nhân số theo số và phần biến theo phần biến)

= -1\(x^3y^2\) 

Tại \(x\)= -1 ; \(y\) = - 4  ta có

-1.(-1)\(^3\).(-4)\(^2\)= -1.(-1). 16 = 16 

Vậy tại x= -1 ; y = - 4 biểu thức -2\(x^2+xy^2\) là 16

\(-x^2y+2y^2\)               (\(-x^2y\) là \(-1x^2y\))

= (-1+2). \(x^2.\left(y.y^2\right)\)

= 1\(x^2y^3\)

Tại  x= 0 ; y = - 2 ta có 

1.\(\left(0\right)^2.\left(-2\right)^3\)= 1. 0. -8 = 0                  (0 nhân với số nào cũng bằng 0)

Vậy tại x= 0 ; y = - 2 biểu thức \(-x^2y+2y^2\) là 0

NHỮNG CHỖ NÀO CÓ IN ĐẬM VÀ NGHIÊNG LÀ KHÔNG GHI NHA

\(x^3+y^3-2x^2-2y^2+3xy\left(x+y\right)-4xy+3\left(x+y\right)+10=\left[x^3+y^3+3xy\left(x+y\right)\right]-2\left(x^2+2xy+y^2\right)+3\left(x+y\right)+10=\left(x+y\right)^3-2\left(x+y\right)^2+3\left(x+y\right)+10=5^3-2.5^2+3.5+10=100\)

Đoạn:

2x
2 + 2y
2 − 3z
2= -100 là như thế nào bạn nhỉ?

Bạn viết lại đề để mọi người hiểu hơn nhé.

a) cho A(x) = 0

\(=>2x^2-4x=0\)

\(x\left(2-4x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)

b)\(B\left(y\right)=4y-8\)

cho B(y) = 0

\(4y-8=0\Rightarrow4y=8\Rightarrow y=2\)

c)\(C\left(t\right)=3t^2-6\)

cho C(t) = 0

\(=>3t^2-6=0=>3t^2=6=>t^2=2\left[{}\begin{matrix}t=\sqrt{2}\\t=-\sqrt{2}\end{matrix}\right.\)

d)\(M\left(x\right)=2x^2+1\)

cho M(x) = 0

\(2x^2+1=0\Rightarrow2x^2=-1\Rightarrow x^2=-\dfrac{1}{2}\left(vl\right)\)

vậy M(x) vô nghiệm

e) cho N(x) = 0

\(2x^2-8=0\)

\(2\left(x^2-4\right)=0\)

\(2\left(x^2+2x-2x-4\right)=0\)

\(2\left(x-2\right)\left(x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

`e, N(x) = 2x^2 - 8 = 2( x^2 - 4 ) = 2( x-2 )( x + 2 )`

Xét `N(x)=0`

`=> 2(x-2)(x+2)=0`

`=>(x-2)(x+2)=0`

`=>x-2=0` hoặc `x+2=0`

`=>x=2` hoặc `x=-2`

Vậy `x in { +-2 }` là nghiệm của `N(x)` 

a) \(P=3\left(x^2+2xy+y^2\right)-2\left(x+y\right)-100\)

\(P=3\left(x+y\right)^2-2.5-100\)

\(P=3.5^2-110\)

\(P=-35\)

b) \(Q=\left[x^3+y^3+3xy\left(x+y\right)\right]-2\left(x^2+2xy+y^2\right)+3.5+10\)

\(Q=\left(x+y\right)^3-2\left(x+y\right)^2+25\)

\(Q=5^3-2.5^2+25\)

\(Q=100\)

Bạn vui lòng viết đề đầy đủ, và gõ bằng công thức toán để được hỗ trợ tốt hơn.

đề theo mik nhìn 

Áp dụng Bunyakovsky, ta có :

\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)

=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)

=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)

Mấy cái kia tương tự