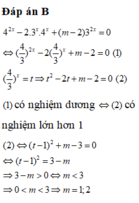Giải phương trình nghiệm nguyên: \(9x^2+12x=4y^2+17\)
NT
Những câu hỏi liên quan
Giải phương trình nghiệm nguyên: \(9x^2+12x=4y^2+17\)
\(9x^2+12x-4y^2-17=0\)
\(\Leftrightarrow\left(3x+2\right)^2-4y^2-21=0\)
\(\Leftrightarrow\left(3x+2y+2\right)\left(3x-2y+2\right)=21\)
Xét
TH1:\(\hept{\begin{cases}3x+2y+2=1\\3x-2y+2=21\end{cases}\Leftrightarrow x=3;y=-5\left(thỏa\right)}\)
TH2:\(\hept{\begin{cases}3x+2y+2=21\\3x-2y+2=1\end{cases}\Leftrightarrow x=3;y=5\left(thỏa\right)}\)
TH3:\(\hept{\begin{cases}3x+2y+2=-1\\3x-2y+2=-21\end{cases}\Leftrightarrow x=\frac{-13}{3};y=5\left(k.thỏa\right)}\)
TH4:\(\hept{\begin{cases}3x+2y+2=-21\\3x-2y+2=-1\end{cases}\Leftrightarrow x=\frac{-13}{3};y=-5\left(k.thỏa\right)}\)
TH5:\(\hept{\begin{cases}3x+2y+2=3\\3x-2y+2=7\end{cases}\Leftrightarrow x=1;y=-1\left(thỏa\right)}\)
TH6:\(\hept{\begin{cases}3x+2y+2=7\\3x-2y+2=3\end{cases}\Leftrightarrow x=y=1\left(thỏa\right)}\)
TH7:\(\hept{\begin{cases}3x+2y+2=-3\\3x-2y+2=-7\end{cases}\Leftrightarrow x=\frac{-7}{3};y=1\left(k.thỏa\right)}\)
TH7:\(\hept{\begin{cases}3x+2y+2=-7\\3x-2y+2=-3\end{cases}\Leftrightarrow x=\frac{-7}{3};y=-1\left(k.thỏa\right)}\)
Vậy \(\left(a;b\right)=\left(3;5\right)=\left(3;-5\right)=\left(1;1\right)=\left(1;-1\right)\)
Đúng 0
Bình luận (0)
Giải phương trình nghiệm nguyên \(x^2+4y^2+28=17\left(x^4+y^4+14y^2+49\right)\)
mày bị ngáo ak. đã xấu còn bị điên. đã bị điên cò học dốt
Đúng 0
Bình luận (0)
y^2+7=z
\(\Leftrightarrow x^2+4z=17\left(x^4+z^2\right)\)Hiển nhiên \(VP\ge VT\) đẳng thức chỉ xẩy ra khi x=z=0
với z=0=> y^2+7=0 vô nghiệm
KL vô nghiệm nguyên
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình
16
x
-
2
.
12
x
+
(
m
-
2
)
.
9
x
0
có nghiệm dương? A. 1 B. 2 C. 4 D. 3
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + ( m - 2 ) . 9 x = 0 có nghiệm dương?
A. 1
B. 2
C. 4
D. 3
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình
16
x
-
2
.
12
x
+
(
m
-
2
)
.
9
x
0
có nghiệm dương A. 1 B. 2 C. 4 D. 3
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + ( m - 2 ) . 9 x = 0 có nghiệm dương
A. 1
B. 2
C. 4
D. 3
Bài 2: Giải các bất phương trình sau và biểu diện tập nghiệm của mỗi bất phương trình trên một trục số
a. 2x – 3 > 3(x – 2) b.12x+1/12 <_ 9x +1/3 - 8x +1/4
/ : phần
a: 2x-3>3(x-2)
=>2x-3>3x-6
=>-x>-3
hay x<3
b: \(\dfrac{12x+1}{12}< =\dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)
=>12x+1<=36x+4-24x-3
=>12x+1<=12x+1(luôn đúng)
Đúng 0
Bình luận (0)
Giải nghiệm nguyên của phương trình :
\( x^2+2xy+y^2+x+4y=0\)
giải phương trình nghiệm nguyên:
\(x^4-4x^3+12x^2-y^2-32x+10y+7=0\)
\(\Leftrightarrow x^4-4x^3+12x^2-32x+32=\left(y-5\right)^2\)
\(\Leftrightarrow\left(x-2\right)^2\left(x^2+8\right)=\left(y-5\right)^2\)
- Với \(x=2\Rightarrow y=5\)
- Với \(x\ne2\Rightarrow x-2\) là ước của \(y-5\)
Đặt \(y-5=n\left(x-2\right)\)
\(\Rightarrow\left(x-2\right)^2\left(x^2+8\right)=n^2\left(x-2\right)^2\)
\(\Rightarrow x^2+8=n^2\)
\(\Rightarrow\left(n-x\right)\left(n+x\right)=8\)
\(\Rightarrow\left[{}\begin{matrix}x=1;n=-3\Rightarrow y=8\\x=-1;n=-3\Rightarrow y=14\\x=1;n=3\Rightarrow y=2\\x=-1;n=3\Rightarrow y=-4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên của phương trình: \(3x^2+4y^2+12x+3y+5=0\)
Giúp mình nhé ai nhank mik tik cho! :D
\(Pt\Leftrightarrow3x^2+12x+4y^2+3y+5=0\)
Coi pt trên là pt bậc 2 ẩn x
Ta có : \(\Delta'=36-12y^2-9y-15\)
\(=-12y^2-9y+21\)
Pt có nghiệm \(\Leftrightarrow\Delta'=-12y^2-9y+21\ge0\)
\(\Leftrightarrow-\frac{7}{4}\le y\le1\)
Mà \(y\inℤ\Rightarrow y\in\left\{-1;0;1\right\}\)
Rồi làm nốt
Đúng 0
Bình luận (0)
a, giải phương trình sau: \(4x^3+4x^2-5x+9=4\sqrt[4]{16x+8}\)
b, chứng minh phương trình sau vô nghiệm trên tập hợp số thực:
\(9x^4+x\left(12x^2+6x-1\right)+\left(x+1\right)\left(9x^2+12x+5\right)+1=0\)
a) Điều kiện xác định \(16x+8\ge0\Leftrightarrow x\ge-\frac{1}{2}.\)
Theo bất đẳng thức Cô-Si cho 4 số ta được
\(4\sqrt[4]{16x+8}=4\sqrt[4]{2\cdot2\cdot2\cdot\left(2x+1\right)}\le2+2+2+2x+1=2x+7\)
Do vậy mà \(4x^3+4x^2-5x+9\le2x+7\Leftrightarrow\left(2x-1\right)^2\left(x+2\right)\le0\).
Vì \(x\ge-\frac{1}{2}\to x+2>0\to\left(2x-1\right)^2\le0\to x=\frac{1}{2}.\)
b. Ta viết phương trình dưới dạng sau đây \(9x^4-21x^3+27x^2+16x+16=0\Leftrightarrow3x^2\left(3x^2-7x+7\right)+4\left(x+2\right)^2=0\)
Vì \(3x^2-7x+7=\frac{36x^2-2\cdot6x\cdot7+49+35}{12}=\frac{\left(6x-7\right)^2+35}{12}>0\) nên vế trái dương, suy ra phương trinh vô nghiệm.
Đúng 0
Bình luận (0)