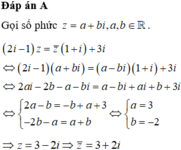Cho số phức z thoa mãn (1+2i)z+(1+2\(\overline{z}\))i=1+3i tìm moodun cua z
MD
Những câu hỏi liên quan
Tìm tất cả các số phức \(z\) thỏa mãn điều kiện:
\(\left|iz-1-3i\right|.\left|\overline{z}+1+i\right|=\left|z^2+\left(-6+2i\right)z+8-6i\right|\) và \(\dfrac{z-3}{z+2}\) là số thuần ảo.
Tìm số phức z thỏa mãn (1 + i)z + (2 - 3i)(1 + 2i) 7 + 3i. A. B. C. D.
Đọc tiếp
Tìm số phức z thỏa mãn (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i.
A. ![]()
B. ![]()
C. ![]()
D. 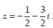
Chọn B.
Ta có: (2 - 3i).(1 + 2i) = 2 + 4i - 3i - 6i2 = 8 + i
Từ giả thiết : (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i nên
(1 + i)z + (8 + i) = 7 + 3i hay (1 + i)z = -1 + 2i

Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
(
2
+
3
i
)
z
-
(
1
+
2
i
)
z
¯
7
-
i
. Tìm mô đun của z. A.
z
1 B.
z...
Đọc tiếp
Cho số phức z thỏa mãn ( 2 + 3 i ) z - ( 1 + 2 i ) z ¯ = 7 - i . Tìm mô đun của z.
A. z =1
B. z =2
C. z = 3
D. z = 5
Đáp án D
Phương pháp:
Đặt z=a+bi, giải phương trình để tìm a, b
Cách giải: ![]()
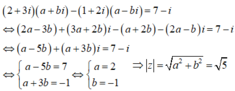
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn (2+3i)z - (1+2i) z = 7 - i. Tìm mô đun của z
A. |z| = 1
B. |z| = 2
C. |z| = 3
D. |z| = 5
Bài tập số 4: Tìm số phức liên hợp overline{Z} và tính modun (|z|) của số phức sau. a, z 2 + 3i b, zleft(2+3iright)^3 c, zdfrac{2+3i}{1-2i} d, zsqrt{2}-dfrac{4}{3}i
Đọc tiếp
Bài tập số 4: Tìm số phức liên hợp \(\overline{Z}\) và tính modun (|z|) của số phức sau.
a, z = 2 + 3i b, \(z=\left(2+3i\right)^3\)
c, \(z=\dfrac{2+3i}{1-2i}\) d, \(z=\sqrt{2}-\dfrac{4}{3}i\)
Cho số phức z thỏa mãn (2+i)z=4-3i Tìm mô đun cua số phức w=iz +2\(\overline{z}\)
gọi z= a + bi \(\left(a,b\in R\right)\)
(2+i)(a+bi)=4-3i
\(\Leftrightarrow\) \(2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
w= i(1-2i) + 2( 1+ 2i) = 4 + 5i
Đúng 0
Bình luận (0)
Mình tưởng tìm moodun của một số \(\sqrt{a^2+b^2}\) chứ. @Nhók Lì Lợm
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn (2+i)z=4-3i Tìm mô đun cua số phức w=iz +2\(\overline{z}\)
Gọi \(z=a+bi\left(a,b\in R\right)\)
\(\left(2+i\right)\left(a+bi=4-3i\right)\)
\(\Leftrightarrow2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
\(w=i\left(1-2i\right)+2\left(1+2i\right)=4+5i\)
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
2
i
−
1
z
z
¯
1
+
i
+
3
i
. Tìm phần ảo của số phức liên hợp của z. A. 2 B. -2 C. 2i D. -2i
Đọc tiếp
Cho số phức z thỏa mãn 2 i − 1 z = z ¯ 1 + i + 3 i . Tìm phần ảo của số phức liên hợp của z.
A. 2
B. -2
C. 2i
D. -2i
Cho số phức z thỏa mãn
2
i
-
1
z
z
¯
1
+
i
+
3
i
Tìm phần ảo của số phức liên hợp của z. A. –2i B. 2i C. –2 D. 2
Đọc tiếp
Cho số phức z thỏa mãn 2 i - 1 z = z ¯ 1 + i + 3 i Tìm phần ảo của số phức liên hợp của z.
A. –2i
B. 2i
C. –2
D. 2