Đề số 2

18.

\(y=a\) là tiệm cận ngang \(\Rightarrow a=-1\)

\(x=-c\) là tiệm cận đứng \(\Rightarrow c=-1\)

\(\Rightarrow y=\dfrac{-x+b}{x-1}\)

Đồ thị hàm số đi qua điểm \(\left(2;0\right)\Rightarrow\dfrac{-2+b}{2-1}=0\Rightarrow b=2\)

\(\Rightarrow T=0\)

19.

\(P=\dfrac{a^{\sqrt{2022}+1+2-\sqrt{2022}}}{a^{\left(\sqrt{2}-2\right)\left(\sqrt{2}+2\right)}}=\dfrac{a^3}{a^{-2}}=a^5\)

20.

\(T=2(a+b)^{-1}.(ab)^{\frac{1}{2}}\left[1+\dfrac{1}{4}\left(\sqrt{\dfrac{a}{b}}-\sqrt{\dfrac{b}{a}} \right)^2 \right]^\frac{1}{2}\)

\(=2(a+b)^{-1}(ab)^{\frac{1}{2}}\)\(\left[1+\dfrac{1}{4}.\dfrac{\left(a-b\right)^2}{ab}\right]^{\dfrac{1}{2}}\)

\(=2(a+b)^{-1}(ab)^{\frac{1}{2}}\)\(\left[\dfrac{a^2+b^2+2ab}{4ab}\right]^{\dfrac{1}{2}}\) 

\(=2(a+b)^{-1}(ab)^{\frac{1}{2}}.\dfrac{a+b}{2(ab)^{\frac{1}{2}}}\)

\(=1\)

21.

Do số mũ \(\dfrac{1}{3}\) không nguyên nên:

ĐKXĐ: \(3x^2-1>0\Rightarrow x\in\left(-\infty;-\dfrac{1}{\sqrt{3}}\right)\cup\left(\dfrac{1}{\sqrt{3}};+\infty\right)\)

ChọnA

Đồ thị hàm số $f(x+2)-1$ thu được khi chúng ta tịnh tiến đồ thị sang trái $2$ đơn vị, sau đó tịnh tiến xuống dưới $1$ đơn vị.

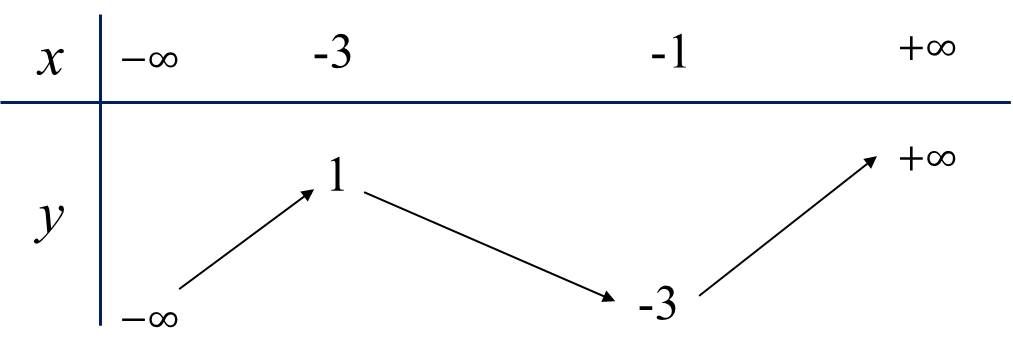
Đây là bảng biến thiên thu được sau khi tịnh tiến. Từ đây, ta suy ra hàm $g(x)=|f(x+2)-1|$ có 5 điểm cực trị.

Chọn B

\(f\left(x\right)=x^2-3x+2\int\limits^1_0f\left(x\right).f'\left(x\right)dx\)

\(\Leftrightarrow f\left(x\right)=x^2-3x+f^2\left(x\right)|^1_0\)

\(\Leftrightarrow f\left(x\right)=x^2-3x+f^2\left(1\right)-f^2\left(0\right)=x^2-3x+C\)

Với \(C=f^2\left(1\right)-f^2\left(0\right)\)

\(f\left(1\right)=C-2\) ; \(f\left(0\right)=C\Rightarrow f^2\left(1\right)-f^2\left(0\right)=\left(C-2\right)^2-C^2=C\)

\(\Rightarrow-4C+4=C\Rightarrow C=\dfrac{4}{5}\)

\(\Rightarrow f\left(x\right)=x^2-3x+\dfrac{4}{5}\)

\(\Rightarrow\int\limits^a_0f\left(x\right)dx=\int\limits^a_0\left(x^2-3x+\dfrac{4}{5}\right)dx=\left(\dfrac{1}{3}x^3-\dfrac{3}{2}x^2+\dfrac{4}{5}x\right)|^a_0\)

\(=\dfrac{a^3}{3}-\dfrac{3a^2}{2}+\dfrac{4a}{5}=\dfrac{4a}{5}\)

\(\Rightarrow\dfrac{a^3}{3}-\dfrac{3a^2}{2}=0\Rightarrow a=\dfrac{9}{2}\)

B.