Tìm phép biến hình biến đồ thị y=x2 thành đồ thị:
a/ y=x2/2
b/ y=x2/4 + 3
TT
Những câu hỏi liên quan
lập bản biến thiên và vẽ đồ thị của hàm số sau:
b) y=x2 - 4x +3
e) y= -x2 + 4x -3
b: Tọa độ đỉnh của (P): y=x2-4x+3 là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-\left(-4\right)}{2}=\dfrac{4}{2}=2\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{\left(-4\right)^2-4\cdot1\cdot3}{4}=-\dfrac{16-12}{4}=-1\end{matrix}\right.\)
Bảng biến thiên:
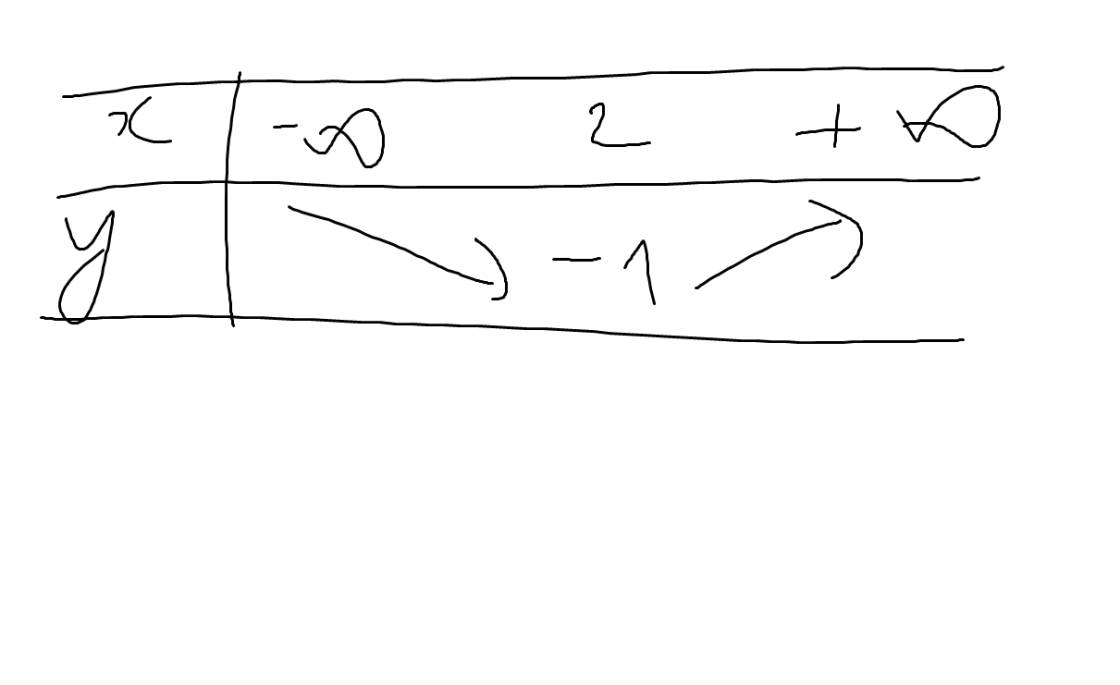
Vẽ đồ thị hàm số:
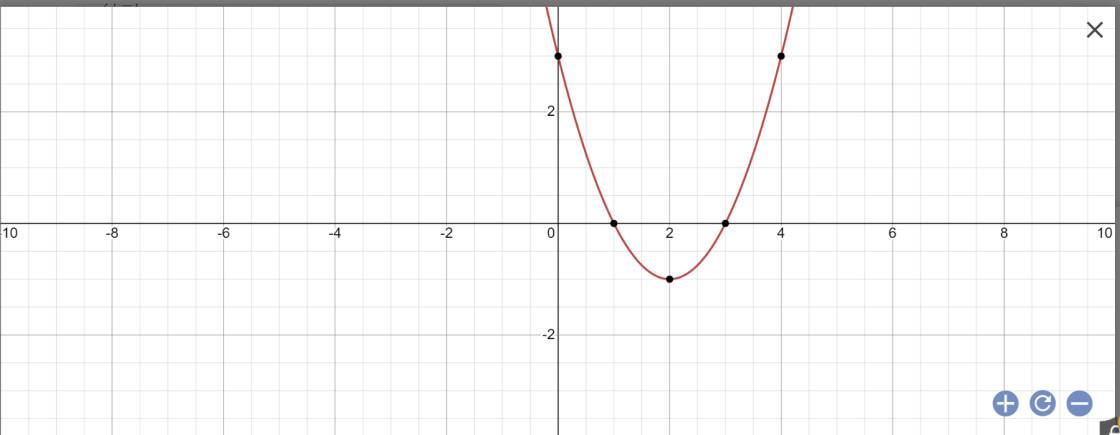
e: Tọa độ đỉnh của (P): y=-x2+4x-3 là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-4}{2\cdot\left(-1\right)}=\dfrac{4}{2}=2\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{4^2-4\cdot\left(-1\right)\cdot\left(-3\right)}{4\cdot\left(-1\right)}=1\end{matrix}\right.\)
Bảng biến thiên:
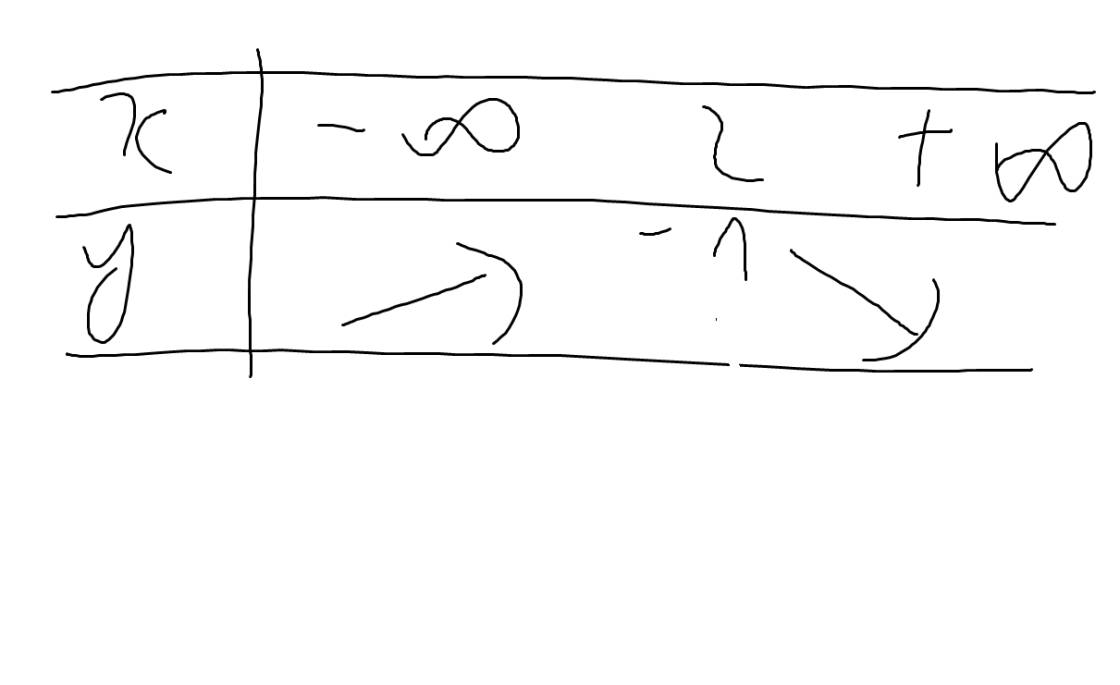
vẽ đồ thị hàm số:
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đồ thị hàm số yf (x) như hình vẽ bên. Hàm số
y
f
(
x
2
-
2
)
-
1
3
x
3
-
x
2
+
3
x
-
4
nghịch biến trên khoảng nào dưới đây ? A.
-
∞...
Đọc tiếp
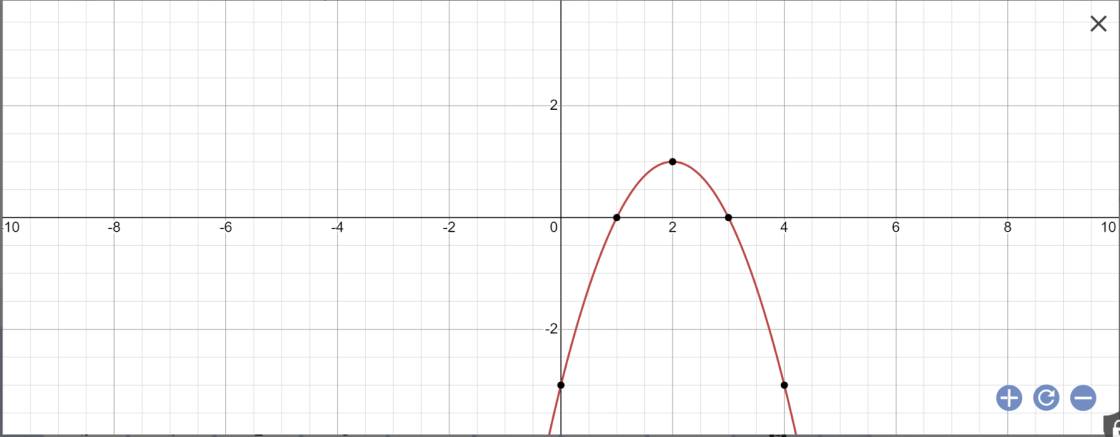
Cho hàm số y=f(x) có đồ thị hàm số y=f '(x) như hình vẽ bên. Hàm số y = f ( x 2 - 2 ) - 1 3 x 3 - x 2 + 3 x - 4 nghịch biến trên khoảng nào dưới đây ?
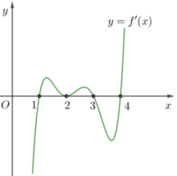
A. - ∞ ; - 3
B. - 3 ; 0
C. 1 ; 3
D. - 3 ; + ∞
Có 
Bất phương trình này khó giải trực tiếp, do vậy ta sẽ chọn x thoả mãn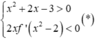 
TH1: Nếu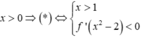 
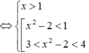
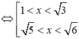
Chọn đáp án C.
TH2: Nếu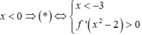 
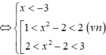
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:a. yx3-3x+2b. yx3+1c. y -x3+3x+1d. y-x3-5x2-9x-4e. yx4-2x2-1f. y -dfrac{x^4}{2}-x2+dfrac{3}{2}g. y2x2-x4
Đọc tiếp
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a. y=x3-3x+2
b. y=x3+1
c. y= -x3+3x+1
d. y=-x3-5x2-9x-4
e. y=x4-2x2-1
f. y= \(-\dfrac{x^4}{2}\)-x2+\(\dfrac{3}{2}\)
g. y=2x2-x4
Cho hàm số y f( x). Đồ thị hàm số y f’(x) như hình bên dưới Hàm số
g
(
x
)
f
(
x
2
+
2
x
+
3
-
x
2
+
2
x...
Đọc tiếp
Cho hàm số y= f( x). Đồ thị hàm số y= f’(x) như hình bên dưới
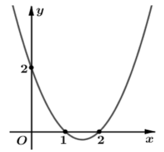
Hàm số g ( x ) = f ( x 2 + 2 x + 3 - x 2 + 2 x + 2 ) đồng biến trên khoảng nào sau đây?
A. ( - ∞ ; - 1 )
B. ( - ∞ ; - 1 / 2 )
C. ( 1 / 2 ; + ∞ )
D. ( - 1 ; + ∞ )
Vẽ bảng biến thiên và đồ thị của hàm số y=x2+|x|
Tìm x để y<=0
Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình bên. Hàm số y = f ( 3 − x 2 ) nghịch biến trên khoảng nào?
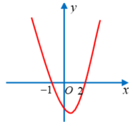
A. (0;2)
B. (-1;2)
C. (1;2)
D. (-2;-1)
Cho hàm số yf(x) được xác định trên R và hàm số ff’(x) có đồ thị như hình vẽ.Tìm khoảng nghịch biến của hàm số
y
f
(
x
2
–
3
)
? A. (-∞;-1) và (0;1) B. (-1;0) C. (-1;0) D. (-1;1)
Đọc tiếp
Cho hàm số y=f(x) được xác định trên R và hàm số f=f’(x) có đồ thị như hình vẽ.
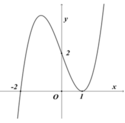
Tìm khoảng nghịch biến của hàm số y = f ( x 2 – 3 ) ?
A. (-∞;-1) và (0;1)
B. (-1;0)
C. (-1;0)
D. (-1;1)
Cho hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ bên dưới. Hàm số
y
3
-
x
2
đồng biến trên khoảng A. (0;1) B. (-1;0) C. (2;3) D. (-2;-1)
Đọc tiếp
Cho hàm số y = f(x). Biết hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Hàm số y = 3 - x 2 đồng biến trên khoảng
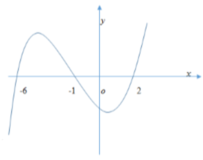
A. (0;1)
B. (-1;0)
C. (2;3)
D. (-2;-1)
Mọi người giúp mình câu c với ạ, làm mãi đáp án nó vẫn sai qatrou T-T
Bài 2: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a/ y = x2 + 6x + 5
b/ y = x2 - 4x
c/ y = -x2 - 2
d/ y = -x2 + 4x - 4
Bài 2:
a:
| x | -∞ | -3 | +∞ |
| y | +∞ | -4 | +∞ |
Đúng 0
Bình luận (0)