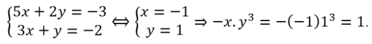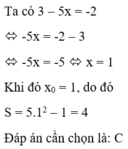Giả sử các số \(5x-y;2x+3y;x+2y\) lập thành một cấp số cộng, còn các số \(\left(y+1\right)^2;xy+1;\left(x-1\right)^2\) lập thành cấp số nhân. Tìm x, y ?
NM
Những câu hỏi liên quan
Giả sử các số x+6y;5x+2y;8x+y lập thành một cấp số cộng, còn các số x+5/3;y-1;2x-3y lập thành cấp số nhân. Tìm x, y ?
Do 3 số... lập thành CSC nên ta có: \(2\left(5x+2y\right)=\left(x+6y\right)+\left(8x+y\right)\)
\(\Leftrightarrow10x+4y=9x+7y\Leftrightarrow x=3y\) (1)
Do 3 số... lập thành CSN nên ta có:
\(\left(y-1\right)^2=\left(x+\frac{5}{3}\right)\left(2x-3y\right)\) (2)
Thế (1) vào (2):
\(\left(y-1\right)^2=\left(3y+\frac{5}{3}\right)\left(6y-3y\right)\)
\(\Leftrightarrow8y^2+7y-1=0\Rightarrow\left[{}\begin{matrix}y=-1\Rightarrow x=-3\\y=\frac{1}{8}\Rightarrow x=\frac{3}{8}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hệ phương trình
5
x
+
2
y
-
3
3
x
+...
Đọc tiếp
Cho hệ phương trình 5 x + 2 y = - 3 3 x + y = - 2
Giả sử (x;y) là nghiệm của hệ phương trình, khi đó - x . y 3 bằng
A. -1.
B. 1
C. 2
D. -2
Giả sử x; y là các số thực dương. Mệnh đề nào sau đây sai? A.
log
2
x
+
y
log
2
x
+
log
2
y
B.
log
2
x
y
1
2
log
2...
Đọc tiếp
Giả sử x; y là các số thực dương. Mệnh đề nào sau đây sai?
A. log 2 x + y = log 2 x + log 2 y
B. log 2 x y = 1 2 log 2 x + log 2 y
C. log 2 x y = log 2 x + log 2 y
D. log 2 x y = log 2 x - log 2 y
Biết F(x) là một nguyên hàm của hàm số
f
x
6
x
2
+
13
x
+
11
2
x
2
+
5
x
+
2
thỏa mãn F(2)7. Giả sử rằng...
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f x = 6 x 2 + 13 x + 11 2 x 2 + 5 x + 2 thỏa mãn F(2)=7. Giả sử rằng F 1 2 = 5 2 + a ln 2 − b ln 5 , trong đó a, b là các số nguyên. Tính trung bình cộng của a và b.
A. 8
B. 3
C. 10
D. 5
Giẳ sử các số
5
x
−
y
,
2
x
+
3
y
,
x
+
2
y
lập thành một cấp số cộng, còn các số
y
+
1
2
,
x
y
+
1
,
x
−
1
2
lập thành cấp số nhân . Hiệu của x,y dương bẳng? A. 1 B. 2 C. 5/3 D. 1...
Đọc tiếp
Giẳ sử các số 5 x − y , 2 x + 3 y , x + 2 y lập thành một cấp số cộng, còn các số y + 1 2 , x y + 1 , x − 1 2 lập thành cấp số nhân . Hiệu của x,y dương bẳng?
A. 1
B. 2
C. 5/3
D. 1/3
5 x − y + x + 2 y = 2 2 x + 3 y y + 1 2 . x − 1 2 = x y + 1 2
⇔ 2 x = 5 y x y + x − y − 1 2 = x y + 1 2 ⇔ 2 x = 5 y x y + x − y − 1 = x y + 1 x y + x − y − 1 = − x y − 1 ⇔ 2 x = 5 y x − y = 2 2 x y + x − y = 0
Ta có x − y = 2 .
Chọn đáp án B.
Đúng 0
Bình luận (0)
Giả sử
x
0
là một số thực thỏa mãn 3 – 5x -2. Tính giá trị của biểu thức S
5
x
0
2
-
1
ta được A. S 1 B. S -1 C. S 4 D. S -6
Đọc tiếp
Giả sử x 0 là một số thực thỏa mãn 3 – 5x = -2. Tính giá trị của biểu thức S = 5 x 0 2 - 1 ta được
A. S = 1
B. S = -1
C. S = 4
D. S = -6
giả sử x, y là các số nguyên dương sao cho A=(x^2+y^2+6)/xy là một số nguyên. CMR A là số lập phương đúng
Cho hàm số y=5x2-4
a) Chứng tỏ : f(x) = f(-x)
b) Giả sử x1<x2<0. Chứng tỏ f(x1)>f(x2)
y=f(x)=5x2 -4
a) f(x) =5x2 -4 = 5(-x)2 -4 = f (-x) ; vì (-x)2 =x 2
b) x1<x2<0 => x1+x2<0 và x1 - x2 <0
f(x1) - f(x2) = (5x12- 4 )- (5x22 -4) = 5(x1-x2)(x1+x2) >0 ( theo trên)
=> f(x1) > f(x2)
Đúng 0
Bình luận (0)
Cho dãy tỉ số bằng nhau: x/y=z/t=u/v(giả sử các tỉ số đã cho đều có nghĩa) suy ra được