| Tình chiều cao của tháp pisa, biết góc nghiêng là 87o1’, bóng tháp nghiêng so với mặt đất là 3m |
Vào thời điểm các tia nắng mặt trời tạo với mặt đất góc nghiêng 32o, một cái tháp có bóng in trên mặt đất dài 24m. Chiều cao của tháp (được làm tròn đến mét) xấp xỉ
Chiều cao của tháp là: \(24.tan32^0\approx15\left(m\right)\)
Một học sinh đứng ở mặt đất cách tháp ăng-ten cao 150m nhìn thấy đỉnh tháp theo một góc nghiêng lên là \(20^0\) và khoảng cách từ mắt đến mặt đất là 1m. Tính chiều cao của tháp ( làm tròn đến mét)
Một em học sinh đứng trên mặt đất dùng giác kế có chiều cao CD = 1,5m nhìn thấy đỉnh ngọn tháp Pisa một góc bằng 38 o , khoảng cách từ vị trí đo đến chân ngọn tháp là DB = 70m (như hình vẽ). Tính chiều cao AB của tháp Pisa ? (Kết quả làm tròn đến mét).
Một cần cẩu có góc nghiêng so với mặt đất nằm ngang là 40° vậy muốn nâng một vật nặng lên cao 6.5 mét thi cần cẩu phải dài bao nhiêu? Biết chiều cao của xe là 2.6 mét
Từ độ cao \(55,8\;{\rm{m}}\) của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất (Hình 18). Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng \(\frac{1}{{10}}\) độ cao mà quả bóng đạt được trước đó. Gọi \({S_n}\) là tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất \(n\) lần. Tính \(\lim {S_n}\).

Gọi (un) là dãy số thể hiện quãng đường di chuyển của quả bóng sau mỗi lần chạm đất.
Ta có: \({u_1} = 55,8;{u_2} = \frac{1}{{10}}.{u_1};{u_3} = {\left( {\frac{1}{{10}}} \right)^2}.{u_1};...;{u_n} = {\left( {\frac{1}{{10}}} \right)^{n - 1}}.{u_1}.\)
Khi đó dãy (un) lập thành một cấp số nhân lùi vô hạn có số hạng đầu u1 = 55,8 và công bội \(q = \frac{1}{{10}}\) thỏa mãn \(\left| q \right| < 1.\)
\( \Rightarrow {S_n} = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{55,8}}{{1 - \frac{1}{{10}}}} = 62\left( m \right)\)
Vậy tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất n lần là 62 m.
Dùng mặt phẳng nghiêng kéo một vật 50kg lên độ cao 3m. Biết chiều dài mặt phẳng nghiêng là 10m. Bỏ quá lực ma sát, tính lực kéo vật trên mặt phẳng nghiêng
Công kéo vật lên là
\(A=10m.h=10.50.3=1500\left(J\right)\)
Lực kéo vật là :
\(F=\dfrac{A}{l}=\dfrac{1500}{10}=150N\)
Một cái cây có bóng trên mặt đất dài 20m . Cho biết tia nắng qua ngọn cây nghiêng 1 góc 30o so với mặt đất . Tính chiều cao của cây ( làm tròn đến mét )
Chiều cao của cây:
\(h=20.tan30^0\approx12\left(m\right)\)
Từ độ cao 63m của tháp nghiêng PISA ở Italia (H.5) người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao mà quả bóng đạt được ngay trướcđó.
Tính độ dài hành trình của quả bóng từ thờiđiểm ban đầu cho đến khi nó nằm yên trên mặt đất.

Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao của lần rơi ngay trước đó và sau đó lại rơi xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
- Thời điểm chạm đất lần thứ nhất là d 1 = 63
- Thời điểm chạm đất lần thứ hai là:
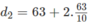
- Thời điểm chạm đất lần thứ ba là:
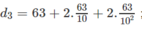
- Thời điểm chạm đất lần thứ tư là:
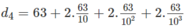
....
- Thời điểm chạm đất lần thứ n (n > 1) là
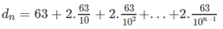
(Có thể chứng minh khẳng định này bằng quy nạp).
Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến khi nằm yên trên mặt đất là :
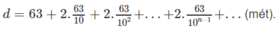
Vì 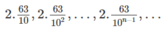
là một cấp số nhân lùi vô hạn, công bội q = 1/10 nên ta có
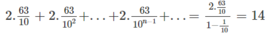
Vậy
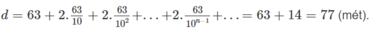
tháp pisa cap 57 mét và nghiêng một góc 3.9 độ tính theo phương thẳng đứng là công trình nổi tiếng ở nước Ý. Nếu đứng ở đỉnh tháp và thả một vật rơi tự do theo phương thẳng đứng thì vật đó cách tâm của đáy tháp là bao nhiêu mét?