a) viết phương trình đường tròn tiếp xúc với 2 trục tọa độ và đi qua điểm (2,1) ; b) viết phương trình đường tròn đi qua 2 điểm (1,1) , (1,4) và tiếp xúc với trục Ox .
BT
Những câu hỏi liên quan
a) viết phương trình đường tròn tiếp xúc với 2 trục tọa độ và đi qua điểm (2,1) ; b) viết phương trình đường tròn đi qua 2 điểm (1,1) , (1,4) và tiếp xúc với trục Ox .
a) viết phương trình đường tròn tiếp xúc với 2 trục tọa độ và đi qua điểm (2,1) ; b) viết phương trình đường tròn đi qua 2 điểm (1,1) , (1,4) và tiếp xúc với trục Ox .
a) viết phương trình đường tròn tiếp xúc với 2 trục tọa độ và đi qua điểm (2,1) ; b) viết phương trình đường tròn đi qua 2 điểm (1,1) , (1,4) và tiếp xúc với trục Ox .
a) viết phương trình đường tròn tiếp xúc với 2 trục tọa độ và đi qua điểm (2,1) ; b) viết phương trình đường tròn đi qua 2 điểm (1,1) , (1,4) và tiếp xúc với trục Ox .
a) viết phương trình đường tròn tiếp xúc với 2 trục tọa độ và đi qua điểm (2,1) ; b) viết phương trình đường tròn đi qua 2 điểm (1,1) , (1,4) và tiếp xúc với trục Ox .
Gọi I(a,b) là tâm của đường tròn
vì đường tròn tiếp xúc với 2 trục tọa độ nên tâm I nằm trên 1 trong các tia phân giác của các trục, nói cách khác là I cách đều hai trục tọa độ => |a| = |b|
nhận xét: đường tròn tiếp xúc với 2 trục tọa độ nên cả hình tròn nằm trong 1 trong 4 góc của hệ trục, lại có A(2, -1) thuộc phần tư thứ IV => tâm I thuộc phần tư thứ IV => a > 0, b < 0
như vậy tọa độ tâm là I(a, -a), bán kính R = a, với a > 0
ptrình đường tròn: (x-a)² + (y+a)² = a²
A(2, -1) thuộc đtròn <=> (2-a)² + (-1+a)² = a² <=> a² - 6a + 5 = 0 <=> a = 1 hoặc a = 5
Vậy có 2 đường tròn thỏa yêu cầu là: (x-1)² + (y+1)² = 1 hoặc (x-5)² + (y-5)² = 25
Đúng 0
Bình luận (0)
bn ơi , điểm có tọa độ là (2,1) mà bn , nhầm rùi kìa
Đúng 0
Bình luận (0)
Bạn ơi,tại bạn này chép lời giải trên mạng nên chưa kịp sửa.
Đúng 0
Bình luận (0)
a) viết phương trình đường tròn tiếp xúc với 2 trục tọa độ và đi qua điểm (2,1) ; b) viết phương trình đường tròn đi qua 2 điểm (1,1) , (1,4) và tiếp xúc với trục Ox .
Đường tròn (C) đi qua điểm A( 2;4) và tiếp xúc với các trục tọa độ có phương trình là: A. (x-2) 2+ ( y-2) 2 4 hoặc (x-10) 2+ (y-10) 2100 B. (x+2) 2+ ( y-2) 2 4 hoặc (x-2) 2+ ( y-2) 2 4 C. (x-2) 2+ ( y+2) 2 4 hoặc (x-2) 2+ ( y-2) 2 4 D. Đáp án khác
Đọc tiếp
Đường tròn (C) đi qua điểm A( 2;4) và tiếp xúc với các trục tọa độ có phương trình là:
A. (x-2) 2+ ( y-2) 2= 4 hoặc (x-10) 2+ (y-10) 2=100
B. (x+2) 2+ ( y-2) 2= 4 hoặc (x-2) 2+ ( y-2) 2= 4
C. (x-2) 2+ ( y+2) 2= 4 hoặc (x-2) 2+ ( y-2) 2= 4
D. Đáp án khác
Đáp án A
Gọi phương trình đường tròn (C) : (x-a)2+ (y- b) 2= R2
Do (C) tiếp xúc với các trục tọa độ nên ![]() mà điểm A( 2; 4) thuộc (C) nằm trong góc phần tư thứ nhất nên I( a; b) cũng ở góc phần tư thứ nhất.
mà điểm A( 2; 4) thuộc (C) nằm trong góc phần tư thứ nhất nên I( a; b) cũng ở góc phần tư thứ nhất.
Suy ra a= b= R > 0.
Vậy (C) : (x-a) 2+ ( y-a) 2= a2.
Do A thuộc C nên ( 2-a) 2+ (4-a) 2 = a2 hay a2-12a + 20 = 0
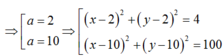
Đúng 0
Bình luận (0)
Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và đi qua điểm \(A(4;2)\)
Gọi tâm của đường tròn là điểm \(I(a;b)\)
Ta có: \(IA = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} ,d\left( {I,Ox} \right) = b,d\left( {I,Oy} \right) = a\)
Giải hệ phương trình \(\left\{ \begin{array}{l}d\left( {I,Ox} \right) = IA\\d\left( {I,Oy} \right) = IA\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \\a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \end{array} \right.\)
Thay \(a = b\) vào phương trình \(a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \) ta có:
\(\begin{array}{l}a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {a - 2} \right)}^2}} \\ \Rightarrow {a^2} = {\left( {a - 4} \right)^2} + {\left( {a - 2} \right)^2}\\ \Rightarrow {a^2} - 12a + 20 = 0\\ \Rightarrow \left[ \begin{array}{l}a = 10\\a = 2\end{array} \right. \end{array}\)
Với \(a = b = 2\) ta có phương trình đường tròn (C) là: \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\)
Với \(a = b = 10\) ta có phương trình đường tròn (C) là: \({\left( {x - 10} \right)^2} + {\left( {y - 10} \right)^2} = 100\)
Đúng 0
Bình luận (0)
Phương trình đường tròn tiếp xúc với hai trục tọa độ và đi qua điểm (2;1) có thể là: A. (x + 1
)
2
+ (y + 1
)
2
1 B. (x - 1
)
2
+ (y - 1
)
2
1 C. (x + 5
)
2
+ (y - 5
)
2
1 D. (x + 5
)
2
...
Đọc tiếp
Phương trình đường tròn tiếp xúc với hai trục tọa độ và đi qua điểm (2;1) có thể là:
A. (x + 1 ) 2 + (y + 1 ) 2 = 1
B. (x - 1 ) 2 + (y - 1 ) 2 = 1
C. (x + 5 ) 2 + (y - 5 ) 2 = 1
D. (x + 5 ) 2 + (y - 5 ) 2 = 25
Đáp án: B
Vì đường tròn tiếp xúc với hai trục tọa độ và đi qua điểm (3;1) nên đường tròn sẽ nằm ở góc phần tư thứ nhất ⇒ I(a;a), R = a (a > 0)
⇒ (x - a ) 2 + (y - a ) 2 = a 2
Vì điểm (3;1) thuộc đường tròn
⇒ (2 - a ) 2 + (1 - a ) 2 = a 2 ⇔ a 2 - 6a + 5 = 0
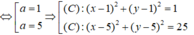
Đúng 0
Bình luận (0)



