viết phương trình đường thẳng song song và cách đường thẳng ax+by+c=0 một khoảng bằng h cho trước .
BT
Những câu hỏi liên quan
Cho đường thẳng (delta): 3x - 4y + 6 = 0; A (4;1) B (-2;3)
a. viết phương trình đường thẳng (d) song song với (Delta) và cách (Delta) một khoảng bằng 3
b. viết phương trình đường thẳng (d2) đi qua A và hợp với (Delta) một góc 45°
Xem chi tiết
a.
Gọi \(M\left(x;y\right)\in d\)
\(\Rightarrow d\left(M;\Delta\right)=3\Leftrightarrow\dfrac{\left|3x-4y+6\right|}{\sqrt{3^2+4^2}}=3\)
\(\Leftrightarrow\left|3x-4y+6\right|=15\Rightarrow\left[{}\begin{matrix}3x-4y+21=0\\3x-4y-9=0\end{matrix}\right.\)
b.
Giả sử đường thẳng (d2) có dạng \(a\left(x+2\right)+b\left(y-3\right)=0\Leftrightarrow ax+by+2a-3b=0\) (1)
\(\dfrac{\left|3.a-4b\right|}{5\sqrt{a^2+b^2}}=\dfrac{1}{\sqrt{2}}\Leftrightarrow2\left(3a-4b\right)^2=25a^2+25b^2\)
\(\Leftrightarrow7a^2+48ab-7b^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}7a=b\\a=-7b\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(1;7\right);\left(7;-1\right)\)
\(\Rightarrow...\) (bạn tự thế vào (1) và rút gọn)
Đúng 2
Bình luận (0)
Cho đường thẳng ∆: - 4x + 3y = 0. Phương trình các đường thẳng song song với ∆ và cách ∆ một khoảng bằng 3 là:
A. -4x + 3y ± 3 = 0
B. -4x + 3y ± 21 = 0
C. 4x - 3y ± 15 = 0
D. -4x + 3y ± 12 = 0
Phương trình đường thẳng song song với ∆ có dạng – 4x + 3y + c = 0. Áp dụng công thức khoảng cách giữa hai đường thẳng song song ta có
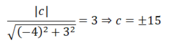
Đáp án C
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng d song song với đường thẳng d':3x-4y+12=0 và cách điểm A một khoảng bằng 2
Cho đường thẳng d: 3x-4y + 20. Có đường thẳng a và b cùng song song với d và cách d một khoảng bằng 1. Hai đường thẳng đó có phương trình là: A. 3x+ 4y- 1 0 ; 3x+ 4y + 5 0 B. 3x-4y+7 0 ; 3x-4y-3 0 C. 3x+ 4y-3 0 ; 3x+ 4y+ 7 0 D.3x- 4y+ 6 0; 3x-4y -4 0
Đọc tiếp
Cho đường thẳng d: 3x-4y + 2=0. Có đường thẳng a và b cùng song song với d và cách d một khoảng bằng 1. Hai đường thẳng đó có phương trình là:
A. 3x+ 4y- 1= 0 ; 3x+ 4y + 5= 0
B. 3x-4y+7= 0 ; 3x-4y-3= 0
C. 3x+ 4y-3= 0 ; 3x+ 4y+ 7= 0
D.3x- 4y+ 6= 0; 3x-4y -4= 0
Giả sử đường thẳng ∆ song song với d : 3x- 4y+2= 0
Khi đó ; ∆ có phương trình là ∆ : 3x-4y +C= 0.
Lấy điểm M( -2 ; -1) thuộc d.

Do đó ; 2 đường thẳng thỏa mãn là:3x – 4y + 7 = 0 và 3x – 4y – 3 = 0
Chọn B
Đúng 0
Bình luận (0)
Cho đường thẳng d: x- 2y + 20.Viết phương trình các đường thẳng song song với d và cách d một đoạn bằng
5
là: A. x-2y- 30; x-2y+ 7 0 B.x- 2y+ 3 0; x-2y+7 0 C. x+ 2y- 3 0; x+2y+7 0 D.x- 2y+ 1 0; x-2y+ 7 0
Đọc tiếp
Cho đường thẳng d: x- 2y + 2=0.Viết phương trình các đường thẳng song song với d và cách d một đoạn bằng 5 là:
A. x-2y- 3=0; x-2y+ 7= 0
B.x- 2y+ 3= 0; x-2y+7= 0
C. x+ 2y- 3= 0; x+2y+7= 0
D.x- 2y+ 1= 0; x-2y+ 7= 0
Đáp án A
Gọi ∆ là đường thẳng song song với d thỏa ,mãn đầu bài
Do ∆ song song với đường thẳng d nên đường thẳng ∆ có dạng:
∆: x- 2y+ c= 0
Theo giả thiết: d d ; ∆ = 5 n ê n c - 2 = 5
Suy ra:c= 7 hoặc c= -3
Vậy có 2 đường thẳng thỏa mãn là : x- 2y+ 7 =0 và x- 2y – 3= 0
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho điểm A(0; -2) và đường thẳng \(\Delta \): x + y - 4 = 0.
a) Tính khoảng cách từ điểm A đến đường thẳng \(\Delta \).
b) Viết phương trình đường thẳng a đi qua điểm M(-1; 0) và song song với \(\Delta \).
c) Viết phương trình đường thẳng b đi qua điểm N(0; 3) và vuông góc với \(\Delta \)
a) Khoảng cách từ điểm A đến đường thẳng \(\Delta \) là: \(d\left( {A,\Delta } \right) = \frac{{\left| {0 - 2 - 4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = 3\sqrt 2 \).
b) Ta có: \(\overrightarrow {{n_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\). Phương trình đường thẳng a là:
\(1\left( {x + 1} \right) + 1\left( {y - 0} \right) = 0 \Leftrightarrow x + y + 1 = 0\)
c) Ta có: \(\overrightarrow {{u_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\).Từ đó suy ra \(\overrightarrow {{n_b}} = \left( {1; - 1} \right)\). Phương trình đường thẳng b là:
\(1\left( {x - 0} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow x - y + 3 = 0\)
Đúng 0
Bình luận (0)
Cho d: 3x - y + 1 = 0. Phương trình đường thẳng song song với d và cách d một khoảng bằng 10 là:
A. 3x - y + 11 = 0
B. 3x - y - 9 = 0
C. Cả A và B đều đúng
D. Cả A và B đều sai
Đáp án: C
Gọi d’ là đường thẳng song song với d và cách d một khoảng bằng 10
Vì d’//d nên d’ có dạng: 3x - y + c = 0, (c ≠ 1)
Lấy M(0;1) ∈ d. Vì d’ cách d một khoảng bằng 10 nên:
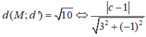
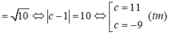
Vậy d': 3x - y + 11 = 0 hoặc d': 3x - y - 9 = 0
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy cho điểm A(3;5) và đường thẳng Δ có phương trình:
2x - y + 3 = 0.
a) viết phương trình đường thẳng d đi qua điểm A và song song với Δ
b) viết phương trình đường tròn tâm A tiếp xúc với đường thẳng Δ
c) tìm điểm B trên Δ cách điểm A(3;5) một khoảng cách bằng 5

