cho hình bình hành ABCD có AB = 4 , BC = 5 , BD = 7 .Tính AC
BT
Những câu hỏi liên quan
Cho hình bình hành ABCD có BD vuông góc với BC. Biết AB=a, góc A = α . Tính diện tích hình bình hành ABCD theo a và α
Cho hình bình hành ABCD như Hình 7.a) Hãy đo rồi so sánh cạnh AB và CD; cạnh BC và AD.b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không?C) AC và BD được gọi là hai đường chéo của hình bình hành.Hai đường chéo AC và BD cắt nhau tại O. Hãy so sánh OA và OC; OB và OD.
Đọc tiếp
Cho hình bình hành ABCD như Hình 7.
a) Hãy đo rồi so sánh cạnh AB và CD; cạnh BC và AD.
b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không?
C) AC và BD được gọi là hai đường chéo của hình bình hành.
Hai đường chéo AC và BD cắt nhau tại O. Hãy so sánh OA và OC; OB và OD.
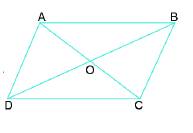
a) AB=CD; BC=AD.
b) Hai cặp cạnh AB và CD song song với nhau, BC và AD song song với nhau.
c) Sử dụng thước đo các cạnh ta thấy OA=OC; OB=OD.
Đúng 0
Bình luận (0)
Hình bình hành ABCD có cạnh AB=8cm, khoảng cách từ giao điểm O hai đường chéo AC và BD đến AB,
BC lần lượt bằng 3cm; 4cm.
a) Tính diện tích hình bình hành.
b) Tính độ dài cạnh BC.
Cho hình bình hành ABCD
a) Chứng minh \(2\left( {A{B^2} + B{C^2}} \right) = A{C^2} + B{D^2}\)
b) Cho \(AB = 4,BC = 5,BD = 7.\) Tính AC.
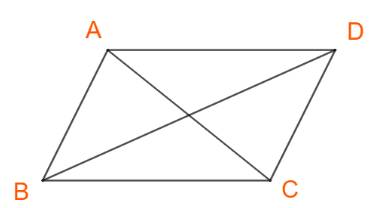
a) Áp dụng định lí cosin ta có:
\(\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos ABC\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos BAD\end{array} \right.\)
Mà \(AD = BC;\cos BAD = \cos ({180^ \circ } - ABC) = - \cos ABC\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos BAD\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos BAD\end{array} \right.\end{array}\)
Cộng vế với vế ta được:
\( A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\)
b) Theo câu a, ta suy ra: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\)
\(\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD biết AB = 5 AD = 9 và đường chéo BD = 11 tính AC
Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2).
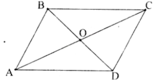
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
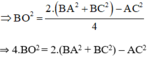
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
Đúng 0
Bình luận (0)
cho hình bình hành ABCD đường chéo BD có AB=5 và AD=4 tìm diện tích của hình bình hành ABCD và hạ AK vuông góc với BD tìm AK
Cho tứ giác ABCD gọi E,F,G,H lần lượt là trung điểm của AB,BC,CD,DA
a,Chứng minh rằng EFGH là hình bình hành
b,Cho AC=8cm và BD=6cm .Hãy tính các cạnh của hình bình hành và chu vi của hình bình hành đó
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình của ΔBAC
Suy ra: EF//AC và \(EF=\dfrac{AC}{2}\left(1\right)\)
Xét ΔADC có
H là trung điểm của AD
G là trung điểm của CD
Do đó: HG là đường trung bình của ΔADC
Suy ra: HG//AC và \(HG=\dfrac{AC}{2}\left(2\right)\)
Từ (1) và (2) suy ra EF//HG và EF=HG
Xét tứ giác EFGH có
EF//HG
EF=HG
Do đó: EFGH là hình bình hành
Đúng 0
Bình luận (0)
hình bình hành ABCD có cạnh AB=4, hai đường chéo AC=6 và BD=8. Tính độ dài cạnh AD
Gọi O là giao của hai đường chéo
Ta có: \(\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}\); \(\overrightarrow{AD}=\overrightarrow{AO}+\overrightarrow{OD}=\overrightarrow{AO}-\overrightarrow{OB}\)
Suy ra : \(\overrightarrow{AB}.\overrightarrow{AD}=AO^2-OB^2=3^2-4^2=-7\)
\(\Leftrightarrow AB^2.AD^2=49\)\(\Leftrightarrow AD^2=\dfrac{49}{16}\Leftrightarrow AD=\dfrac{7}{4}\)
Đúng 1
Bình luận (0)





