Giải giúp e câu a, b vs qj
NT
Những câu hỏi liên quan
Giải giúp e câu a, b vs ạ
Giải giúp e câu 25 vs ạ
Giải giúp e câu 21 vs ạ
Giải giúp e câu 22 vs ạ
Giải giúp e câu này vs ạ 
 giải giúp e câu 2,4,5,6 vs ạ.
giải giúp e câu 2,4,5,6 vs ạ.
Giải giúp e câu 85 vs ạ
Câu 84:
$\sin 3x+2\cos ^2x=1$
$\sin 3x=1-2\cos ^2x=-\cos 2x=\sin (2x-\frac{\pi}{2})$
\(\Rightarrow \left[\begin{matrix} 3x=2x-\frac{\pi}{2}+2k\pi\\ 3x=\frac{3}{2}\pi-2x+2k\pi\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=(2k+\frac{3}{2})\pi\\ x=\frac{2k+\frac{3}{2}}{5}\pi\end{matrix}\right.\) với $k$ nguyên
Nghiệm âm lớn nhất của pt:
$x=\frac{2(-1)+\frac{3}{2}}{5}\pi =\frac{-\pi}{10}$
Đúng 0
Bình luận (0)
84.
\(sin3x+2cos^2x=1\)
\(\Leftrightarrow sin3x+cos2x=0\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-3x\right)+cos2x=0\)
\(\Leftrightarrow2cos\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right).cos\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right)=0\\cos\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{4}-\dfrac{x}{2}=\dfrac{\pi}{2}+k\pi\\\dfrac{\pi}{4}-\dfrac{5x}{2}=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{2}-k2\pi\\x=-\dfrac{\pi}{10}-\dfrac{k2\pi}{5}\end{matrix}\right.\)
\(x=-\dfrac{\pi}{2}-k2\pi< 0\Leftrightarrow k>-\dfrac{1}{4}\Rightarrow k=0\Rightarrow x=-\dfrac{\pi}{2}\)
\(x=-\dfrac{\pi}{10}-k2\pi< 0\Leftrightarrow k>-\dfrac{1}{20}\Rightarrow k=0\Rightarrow x=-\dfrac{\pi}{10}\)
Vậy \(x=-\dfrac{\pi}{10}\) là nghiệm âm lớn nhất
Đúng 0
Bình luận (0)
Câu 85:
ĐKXĐ: $\cos 2x; \cos 3x\neq 0$
$\tan 2x\tan 3x=1$
$\Leftrightarrow \sin 2x\sin 3x=\cos 2x\cos 3x$
$\Leftrightarrow 2\sin 2x\sin 3x=2\cos 2x\cos 3x$
$\Leftrightarrow \cos 5x+\cos x=\cos x-\cos 5x$
$\Leftrightarrow 2\cos 5x=0$
$\Leftrihgtarrow \cos 5x=0$
$\Leftrightarrow x=\frac{1}{5}(\frac{\pi}{2}+k\pi$
$=\frac{2k+1}{10}\pi$
Nghiệm âm lớn nhất: $\frac{-2+1}{10}\pi =\frac{-\pi}{10}$
Đúng 0
Bình luận (0)
Giải giúp e câu 67 vs ạ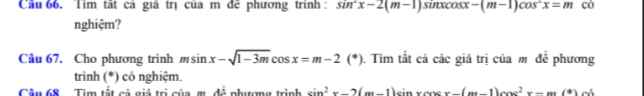
ĐKXĐ: \(1-3m\ge0\Rightarrow m\le\dfrac{1}{3}\) (1)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(m^2+\left(1-3m\right)\ge\left(m-2\right)^2\)
\(\Leftrightarrow1-3m\ge-4m+4\Rightarrow m\ge3\) (2)
Kết hợp (1); (2) \(\Rightarrow\) không tồn tại m thỏa mãn
Đúng 2
Bình luận (0)
Giải giúp e câu 9b vs ạ

