Bài 42: Tìm số tự nhiên n,biết:
a)7^ n = 49
Bài 43: Viết các số sau dưới dạng 1 luỹ thừa:
a)10;100;1000;10000;100...0;(n số 0
Bài 44: So sánh các số sau:
a)3 ^ 200 với 2 ^300
Bài 1: Viết các số, các tích, thương sau dưới dạng luỹ thừa:
a, 8; 125; 27; 64; 81; 625; 1000; 10000000; 1000...000 ( k chữ số 0 )
b, 7 . 7 . 7 7 . 8 . 7 . 25 2 . 3 . 8 . 12 . 24 x.x.y.y.x.y.x 1000.10.10
c, 315 : 35 98 . 32 125 : 53 75 : 343 a12 : a18 (a ≠ 0 )
x7 . x4.x 85 . 23 : 24
a: \(8=2^3\)
\(125=5^3\)
\(27=3^3\)
\(64=8^2\)
\(81=9^2\)
\(1000=10^3\)
\(10000000=10^7\)
1000..000=10k
b: \(7\cdot7\cdot7=7^3\)
\(7\cdot8\cdot7\cdot25=7^2\cdot200=70^2\cdot2^2\)
a) \(2^3;5^3;3^3;4^3;3^4;5^4;10^3;10^7;10^k3^4\)
Viết các tích sau dưới dạng một luỹ thừa:
a) 9.9.9.9.9; b) 10. 10. 10. 10.
c) 5.5.5.25 d) a.a.a.a.a.a
a) 9 . 9 . 9 . 9 . 9 = 95
b) 10 . 10 . 10 . 10 = \(10^4\)
c) 5.5.5.25=5.5.5.5.5=\(5^5\)
d) a.a.a.a.a.a=\(a^6\)
a) 9.9.9.9.9=95 b) 10. 10. 10. 10=104
c) 5.5.5.25=5.5.5.5.5=55 d) a.a.a.a.a.a=a6
viết các tích sau dưới dạng 1 luỹ thừa:
a( 25^20 . 125^4 =
b( x^7 . x^4 . x^3 =
c( 3^6 . 4^6 =
\(a,=5^{40}\cdot5^{12}=5^{52}\\ b,=x^{7+4+3}=x^{14}\\ c,=\left(3\cdot4\right)^6=12^6\)
a) \(25^{20}.125^4=\left(5^2\right)^{20}.\left(5^3\right)^4=5^{40}.5^{12}=5^{40+12}=5^{52}\)
b) \(x^7.x^4.x^3=x^{7+4+3}=x^{14}\)
c) \(3^6.4^6=\left(3.4\right)^6=12^6\)
viết các tích sau dưới dạng 1 luỹ thừa:
a( 25^20 . 125^4 = (52)20 . (53)4 = 540 . 512 = 552
b( x^7 . x^4 . x^3 = x7+4+3 = x14
c( 3^6 . 4^6 = (3.4)6=126
??
Tìm các số từ 1 đến 30 sao cho nó là
a) Bình phương của một số tự nhiên b) Lập phương của một số tự nhiên
Viết các số sau dưới dạng luỹ thừa của 10
100 ; 1000; 10000;1000000 ; 100000000
Tìm các số từ 1 đến 30 sao cho nó là
a) Bình phương của một số tự nhiên b) Lập phương của một số tự nhiên
Viết các số sau dưới dạng luỹ thừa của 10
100 ; 1000; 10000;1000000 ; 100000000
a,1;4;9;16;25
b,1;8;27
c, 100=10^2
1000=10^3
10000=10^4
1000000=10^6
100000000=10^8
Bài 10: Tìm các số nguyên \(x\) biết:
a) \(2x-3\) là bội của \(x+1\)
b) \(x-2\) là ước của \(3x-2\)
Bài 14: Tìm số tự nhiên \(n\) sao cho:
a) \(4n-5\) ⋮ \(2n-1\)
b) \(n^2+3n+1\) ⋮ \(n+1\)
Bài 16: Tìm cặp số tự nhiên \(x\),\(y\) biết:
a) \(\left(x+5\right)\left(y-3\right)=15\)
b) \(\left(2x-1\right)\left(y+2\right)=24\)
c) \(xy+2x+3y=0\)
d) \(xy+x+y=30\)
Bài 10:
a: 2x-3 là bội của x+1
=>\(2x-3⋮x+1\)
=>\(2x+2-5⋮x+1\)
=>\(-5⋮x+1\)
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
b: x-2 là ước của 3x-2
=>\(3x-2⋮x-2\)
=>\(3x-6+4⋮x-2\)
=>\(4⋮x-2\)
=>\(x-2\inƯ\left(4\right)\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)
Bài 14:
a: \(4n-5⋮2n-1\)
=>\(4n-2-3⋮2n-1\)
=>\(-3⋮2n-1\)
=>\(2n-1\inƯ\left(-3\right)\)
=>\(2n-1\in\left\{1;-1;3;-3\right\}\)
=>\(2n\in\left\{2;0;4;-2\right\}\)
=>\(n\in\left\{1;0;2;-1\right\}\)
mà n>=0
nên \(n\in\left\{1;0;2\right\}\)
b: \(n^2+3n+1⋮n+1\)
=>\(n^2+n+2n+2-1⋮n+1\)
=>\(n\left(n+1\right)+2\left(n+1\right)-1⋮n+1\)
=>\(-1⋮n+1\)
=>\(n+1\in\left\{1;-1\right\}\)
=>\(n\in\left\{0;-2\right\}\)
mà n là số tự nhiên
nên n=0
Bài 16:
a: \(\left(x+5\right)\left(y-3\right)=15\)
=>\(\left(x+5\right)\left(y-3\right)=1\cdot15=15\cdot1=\left(-1\right)\cdot\left(-15\right)=\left(-15\right)\cdot\left(-1\right)=3\cdot5=5\cdot3=\left(-3\right)\cdot\left(-5\right)=\left(-5\right)\cdot\left(-3\right)\)
=>\(\left(x+5;y-3\right)\in\left\{\left(1;15\right);\left(15;1\right);\left(-1;-15\right);\left(-15;-1\right);\left(3;5\right);\left(5;3\right);\left(-3;-5\right);\left(-5;-3\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(-4;18\right);\left(10;4\right);\left(-6;-12\right);\left(-20;2\right);\left(-2;8\right);\left(0;6\right);\left(-8;-2\right);\left(-10;0\right)\right\}\)
mà (x,y) là cặp số tự nhiên
nên \(\left(x,y\right)\in\left\{\left(10;4\right);\left(0;6\right)\right\}\)
b: x là số tự nhiên
=>2x-1 lẻ và 2x-1>=-1
\(\left(2x-1\right)\left(y+2\right)=24\)
mà 2x-1>=-1 và 2x-1 lẻ
nên \(\left(2x-1\right)\cdot\left(y+2\right)=\left(-1\right)\cdot\left(-24\right)=1\cdot24=3\cdot8\)
=>\(\left(2x-1;y+2\right)\in\left\{\left(-1;-24\right);\left(1;24\right);\left(3;8\right)\right\}\)
=>\(\left(2x;y\right)\in\left\{\left(0;-26\right);\left(2;22\right);\left(4;6\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(0;-26\right);\left(1;11\right);\left(2;6\right)\right\}\)
mà (x,y) là cặp số tự nhiên
nên \(\left(x,y\right)\in\left\{\left(1;11\right);\left(2;6\right)\right\}\)
c:
x,y là các số tự nhiên
=>x+3>=3 và y+2>=2
xy+2x+3y=0
=>\(xy+2x+3y+6=6\)
=>\(x\left(y+2\right)+3\left(y+2\right)=6\)
=>\(\left(x+3\right)\left(y+2\right)=6\)
mà x+3>=3 và y+2>=2
nên \(\left(x+3\right)\cdot\left(y+2\right)=3\cdot2\)
=>x=0 và y=0
d: xy+x+y=30
=>\(xy+x+y+1=31\)
=>\(x\left(y+1\right)+\left(y+1\right)=31\)
=>\(\left(x+1\right)\left(y+1\right)=31\)
\(\Leftrightarrow\left(x+1\right)\cdot\left(y+1\right)=1\cdot31=31\cdot1=\left(-1\right)\cdot\left(-31\right)=\left(-31\right)\cdot\left(-1\right)\)
=>\(\left(x+1;y+1\right)\in\left\{\left(1;31\right);\left(31;1\right);\left(-1;-31\right);\left(-31;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;30\right);\left(30;0\right);\left(-2;-32\right);\left(-32;-2\right)\right\}\)
mà (x,y) là cặp số tự nhiên
nên \(\left(x,y\right)\in\left\{\left(0;30\right);\left(30;0\right)\right\}\)
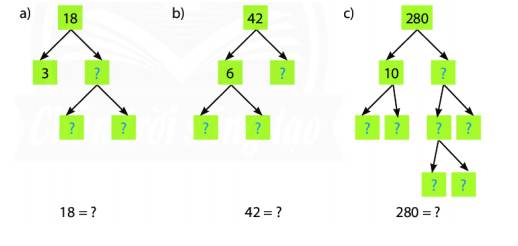
Tìm các số tự nhiên lớn hơn 1 để thay thế dấu trong ô vuông ở mỗi sơ đồ cây dưới đây, rồi viết gọn dạng phân tích ra thừa số nguyên tố của mỗi số 18, 42, 280 bằng cách dùng luỹ thừa.
Viết kết quả các phép tính dưới dạng một luỹ thừa:
a) 76 : 74; b) 1 091100 : 1 091100
a) 76:74 = 76−4 = 72
b) 1091100: 1091100 = 1091100−100 = 10910
a) 76 : 74=72 b) 1 091100 : 1 091100=1
Trong các số sau,số nào là luỹ thừa của một số tự nhiên với số mũ lớn hơn ( chú ý rằng có những số có nhiều cách viết dưới dạng luỹ thừa):
8,16,20,27,60,64,81,90,100
8=2^3
16=4^2
27=3^3
64=8^2
81=9^2
100=10^2
vay cac so co dang luy thua cua 1 so tu nhien lon hon 1 la :8 , 16 , 27 , 64, 81 , 100.
các số dạng lũy thừa của 1 số tự nhiên lớn hơn 1 là:8,16,27,64,81,100