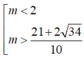cho bpt (x +1)(x+ 2m )>0
tìm m để tập nghiệm của bpt chứa (1;+∞)
Cho bpt \(-x^2-2\left(m-1\right)x+2m-1>0\) . Tìm tất cả các giá trị m để (0;1) là tập con của tập nghiệm bpt \(\left(x_1;x_2\right)\)
\(-x^2-2\left(m-1\right)x+2m-1>0\)
\(\Leftrightarrow x^2+2\left(m-1\right)x-2m+1< 0\)
\(f\left(x\right)=x^2+2\left(m-1\right)x-2m+1\)
Yêu cầu bài toán thỏa mãn khi \(f\left(x\right)=0\) có hai nghiệm phân biệt thỏa mãn \(x_1\le0< 1\le x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m-1\right)^2+2m-1>0\\f\left(1\right)\le0\\f\left(0\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2>0\\1+2\left(m-1\right)-2m+1\le0\\-2m+1\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ge\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow m\ge\dfrac{1}{2}\)
1.Tìm tập nghiệm D của bpt |2x-1|≤x+2.
2.Tìm m để (m+2)x²-3x+2m-3=0 có 2 nghiệm trái dấu.
3.Tìm tập nghiệm của bpt 5x-1>2x/5+3.
4.Tìm tập nghiệm S của bpt (2x+1)² -3(x-3)>4x²+10.
5.Tìm tập nghiệm S của bpt 1<1/1-x.
6.Tìm tập nghiệm S của bpt (x-5)²(x-3)/x+1≤0.
1.
- Với \(x\ge\frac{1}{2}\Rightarrow2x-1\le x+2\Rightarrow x\le3\Rightarrow\frac{1}{2}\le x\le3\)
- Với \(x< \frac{1}{2}\Rightarrow1-2x\le x+2\Rightarrow3x\ge-1\Rightarrow x\ge-\frac{1}{3}\)
Vậy nghiệm của BPT là \(-\frac{1}{3}\le x\le3\)
2.
Để pt có 2 nghiệm trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow\left(m+2\right)\left(2m-3\right)< 0\Rightarrow-2< m< \frac{3}{2}\)
3.
\(5x-1>\frac{2x}{5}+3\Leftrightarrow5x-\frac{2x}{5}>4\Leftrightarrow\frac{23}{5}x>4\Rightarrow x>\frac{20}{23}\)
4.
\(4x^2+4x+1-3x+9>4x^2+10\)
\(\Leftrightarrow x>0\)
5.
\(1< \frac{1}{1-x}\Leftrightarrow\frac{1}{1-x}-1>0\Leftrightarrow\frac{x}{1-x}>0\Rightarrow0< x< 1\)
6.
\(\frac{\left(x-5\right)^2\left(x-3\right)}{x+1}\le0\Rightarrow\left[{}\begin{matrix}x=5\\-1< x\le3\end{matrix}\right.\)
1/ Điều kiện của tham số m để bpt 2x2 + (m-1)x + 1 - m < 0 vô nghiệm
2/ Tìm tất cả các giá trị của m để bpt x2 - (2m-1)x + 2m-2 ≤ 0 có tập nghiệm là 1 đoạn có độ dài = 5.
a/ từ yc đề bài => \(2x^2+\left(m-1\right)x+1-m\ge0\)
nghiệm đúng với mọi x thuộc R
=> \(\Delta\le0\Leftrightarrow\left(m-1\right)^2-4\cdot2\left(1-m\right)\le0\)
\(\Leftrightarrow m^2+2m-7\le0\)
\(\Leftrightarrow m\in\left[-1-2\sqrt{2};-1+2\sqrt{2}\right]\)
b/ x2 - (2m-1)x + 2m-2 = 0
để pt có 2 nghiệm pb => \(\Delta>0\Leftrightarrow\left(2m-1\right)^2-4\left(2m-2\right)>0\)
\(\Leftrightarrow4m^2-12m+9>0\Leftrightarrow\left(2m-3\right)^2>0\Leftrightarrow m\ne\frac{3}{2}\)
=> Gọi 2 nghiệm của pt là x1, x2 (x1<x2)
tập nghiệp của bpt đề cho là: \(S=\left[x_1;x_2\right]\)
theo viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=2m-2\end{matrix}\right.\)
Theo đề ta có: \(\left|x_1-x_2\right|=5\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=25\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=25\)
\(\Leftrightarrow\left(2m-1\right)^2-4\left(2m-2\right)=25\)
\(\Leftrightarrow4m^2-12m-16=0\Leftrightarrow\left[{}\begin{matrix}m=4\\m=-1\end{matrix}\right.\)(tm)
vậy......
cho bpt: (m-2)x2 +2(m+1)x + 2m >= 0 , tìm m để bpt vô nghiệm?
- Với \(m=2\) BPT luôn có nghiệm \(x\ge-\frac{2}{3}\) (ktm)
- Với \(m\ne2\) để BPT vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}m-2< 0\\\Delta'=\left(m+1\right)^2-2m\left(m-2\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\-m^2+6m+1< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m< 2\\\left[{}\begin{matrix}m>3+\sqrt{10}\\m< 3-\sqrt{10}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m< 3-\sqrt{10}\)
1. Biết rằng tập nghiệm của bpt \(\sqrt{2x-4}-2\sqrt{2-x}\ge\dfrac{6x-4}{5\sqrt{x^2+1}}\) là \(\left[a;b\right]\) . Tính P=3a-2b
2. Tính tổng các giá trị nguyên dương của m để tập nghiệm của bpt \(\sqrt{\dfrac{m}{72}x^2+1}< \sqrt{x}\) có chứa đúng 2 số nguyên
1.
ĐKXĐ: \(x=2\)
Xét \(x=2\), bất phương trình vô nghiệm
\(\Rightarrow\) bất phương trình đã cho vô nghiệm
\(\Rightarrow\) Không tồn tại \(a,b\) thỏa mãn
Đề bài lỗi chăng.
Điều kiện của m để bpt: (2m+1)x+ m-5 ≥ 0 nghiệm đúng với mọi x: 0 < x < 1
A. -1/2 < m < 5
B. m = 5
C. m = 5 và m = -1/2
D. m ≥ 5
Chọn D
Bpt đã cho tương đương với ( 2m+1) x ≥ 5-m (*)
TH1: Với m> -1/2, bpt (*) trở thành: 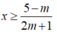
Tập nghiệm của bpt là 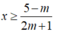
Để bpt đã cho nghiệm đúng với mọi x:
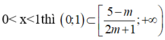
Hay 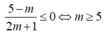
TH2: nếu m= -1/2 , bpt (*) trở thành: 0x ≥ 5+1/2
Bpt vô nghiệm => không có m thòa mãn
TH3: Với m< -1/2, bpt (*) trở thành: 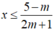
Tập nghiệm của bpt là 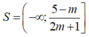
Để bpt đã cho nghiệm đúng với 0< x< 1 thì
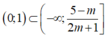
Hay 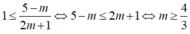
Kết hợp điều kiện m< -1/2 nên không có m thỏa mãn
Vậy với m≥ 5, bất phương trình đã cho nghiệm đúng với mọi x: 0< x< 1
1. Tìm tập nghiệm của bất pt |2x-5|<3?
2. Tất cả các giá trị của x thỏa mãn|x-1|<1 là..?
3. Nghiệm của bpt |2x-3|≤1 là?
4. Bpt |3x-4| ≤2 có nghiệm là?
5. Cho biểu thức f(x)=2x-4. Tập hợp các giá trị của x để f(x) ≥0 là..?
6. Cho biểu thức f(x)= 1/3x-6 tập hợp tất cả các gtrị của x để f(x)≤0 là?
7. Cho bthức f(x)=(2-x/x+1) +2. Tập hợp tất cả các giá trị của X thỏa mãn bpt f(x)<0 là?
8. Cho biểu thức f(x)=1- (2-x/3x-2). Tập hợp tất cả các gtrị của X thỏa mãn bpt f(x)≤0 là?
9. Tập nghiệm của bpt (x-1/x-3)-1<0 là?
10. Số x=2 là nghiệm của bpt nào sau đây:
a) 4-X<1 b) 2X+1<3
c) 3X-7>X d)5X-2>3
11. Tập nghiệm của bpt -4x+1/3x+1≤-3 là?
12. Với X thuộc tập hợp nào thì nhị thức bật nhất f(x)-(x-1)(x+3) không âm?
13. Tập nghiệm S=(-4;5) là tập nghiệm của bpt nào dưới đây:
a)(x+4)(x+5)<0
b)(x+4)(5x-25)<0
c)(x+4)(5x-25)≥0
d) (x-4)(x-5) <0
14. Tổng các tập nghiệm của bpt (x+3)(x-1)≤ 0 là?
GIẢI RA HẾT DÙM EM VỚI Ạ :((
1. Tìm tập nghiệm của bất pt |2x-5|<3?
2. Tất cả các giá trị của x thỏa mãn|x-1|<1 là..?
3. Nghiệm của bpt |2x-3|≤1 là?
4. Bpt |3x-4| ≤2 có nghiệm là?
5. Cho biểu thức f(x)=2x-4. Tập hợp các giá trị của x để f(x) ≥0 là..?
6. Cho biểu thức f(x)= 1/3x-6 tập hợp tất cả các gtrị của x để f(x)≤0 là?
7. Cho bthức f(x)=(2-x/x+1) +2. Tập hợp tất cả các giá trị của X thỏa mãn bpt f(x)<0 là?
8. Cho biểu thức f(x)=1- (2-x/3x-2). Tập hợp tất cả các gtrị của X thỏa mãn bpt f(x)≤0 là?
9. Tập nghiệm của bpt (x-1/x-3)-1<0 là?
10. Số x=2 là nghiệm của bpt nào sau đây:
a) 4-X<1 b) 2X+1<3
c) 3X-7>X d)5X-2>3
11. Tập nghiệm của bpt -4x+1/3x+1≤-3 là?
12. Với X thuộc tập hợp nào thì nhị thức bật nhất f(x)-(x-1)(x+3) không âm?
13. Tập nghiệm S=(-4;5) là tập nghiệm của bpt nào dưới đây:
a)(x+4)(x+5)<0
b)(x+4)(5x-25)<0
c)(x+4)(5x-25)≥0
d) (x-4)(x-5) <0
14. Tổng các tập nghiệm của bpt (x+3)(x-1)≤ 0 là?
GIẢI RA HẾT DÙM EM VỚI Ạ :((
Tìm m để bpt 2x2- (2m+1) x+ m2-2m+2≤ 0 nghiệm đúng với mọi x ∈ 1 2 ; 2
A. 2 ≤ m ≤ 21 + 2 34 10
B. m ≤ 21 + 2 34 10
C. m ≥ 2
D.