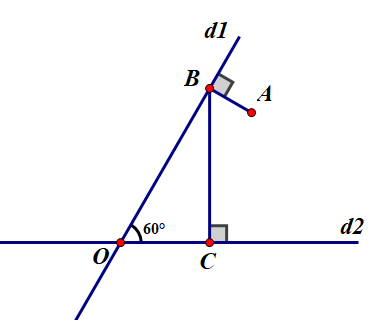
Vẽ lại hình 11 và nói rõ trình tự vẽ hình
MT
Những câu hỏi liên quan
Vẽ lại hình 11 và nói rõ trình tự vẽ hình
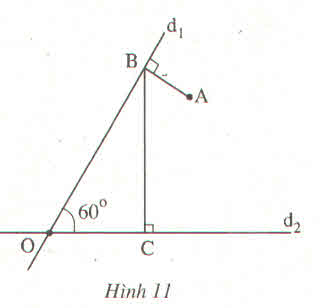
Chú ý : Có thể vẽ hình theo nhiều trình tự khác nhau

vẽ góc d1Od2 bằng 60 độ
lấy A bất kì nằm trong góc d1Od2
kẻ AB vuông góc với d1O tại B
từ B kẻ BC vuông góc với Od2 tại C
Đúng 0
Bình luận (0)

Cách vẽ: Vẽ đường thẳng d1 và d2 cắt nhau tại O sao cho \(\widehat{d_1Od_2=60^0}\).Vẽ A nằm trong \(\widehat{d_1}Od_2\) .Qua A ,vẽ đoạn thẳng AB vuông góc với đường thẳng d1 tại điểm B. Qua B, vẽ đoạn thẳng BC vuông góc với đường thẳng d2 tại C.
Đúng 0
Bình luận (0)
-Vẽ hai đường thẳng \(d_1,d_2\)cắt nhau tại O và tạo thành góc 60 độ.
-Lấy điểm B tuỳ sỹ nằm trên tia \(Od_1\).
-Vẽ đoạn thẳng BC vuông góc với tia \(Od_2\), sao cho điểm C nằm trên tia \(Od_2\).
- Vẽ đoạn thẳng BA vuông góc với tia \(Od_1\), sao cho điểm A nằm trong góc \(d_1Od_2\)
Đúng 0
Bình luận (0)
Nói rõ trình tự vẽ hình 11
hình 11 ở bài 19 trang 87 sách toán 7 tập 1
Nói rõ trình tự vẽ hình

Vẽ đường thẳng d1 và đường thẳng d2 ; 2 đường thẳng này cắt nhau tại O tạo thành một góc \(\widehat{d_1Od_2}=60^o\)
Lấy một điểm A nằm trong góc d1Od2; hạ đường vuông góc từ A đến d1, cắt d1 tại B. Từ B lại hạ đường vuông góc đến d2, cắt d2 tại C
Đúng 0
Bình luận (1)
Cho một hình tròn.Hãy vẽ 4 đường thẳng để chia hình tròn cho trước đó thành 11 phần.Nêu rõ cách vẽ và giải thích vì sao 4 đường thẳng đó lại chia hình tròn đó thành 11 phần?
11. cho đường thẳng d và điểm O thuộc d . vẽ đường thẳng d đi qua O và vuông góc với d . nói rõ cách vẽ và cách sử dụng công cụ ( êke , thước kẻ ) để vẽ .12. cho đường thẳng d và điểm O nằm ngoài đường thẳng d . chỉ sử dụng êke , hãy vẽ đường thẳng d đi qua O và vuông góc với d . nói rõ cách vẽ15 . cho đoạn thẳng AB dài 24mm . hãy vẽ đường trung trực của đoạn thẳng ấy . nói rõ cách vẽChú ý : các bạn khỏi vẽ hình , chỉ cần giúp mik nói rõ cách vẽ là ok rồi cảm ơn nhìu và làm nhanh giùm em ngày m...
Đọc tiếp
11. cho đường thẳng d và điểm O thuộc d . vẽ đường thẳng d' đi qua O và vuông góc với d . nói rõ cách vẽ và cách sử dụng công cụ ( êke , thước kẻ ) để vẽ .
12. cho đường thẳng d và điểm O nằm ngoài đường thẳng d . chỉ sử dụng êke , hãy vẽ đường thẳng d' đi qua O và vuông góc với d . nói rõ cách vẽ
15 . cho đoạn thẳng AB dài 24mm . hãy vẽ đường trung trực của đoạn thẳng ấy . nói rõ cách vẽ
Chú ý : các bạn khỏi vẽ hình , chỉ cần giúp mik nói rõ cách vẽ là ok rồi cảm ơn nhìu và làm nhanh giùm em ngày mai em phải nộp
11. cho đường thẳng d và điểm O thuộc d . vẽ đường thẳng d đi qua O và vuông góc với d . nói rõ cách vẽ và cách sử dụng công cụ ( êke , thước kẻ ) để vẽ . 12. cho đường thẳng d và điểm O nằm ngoài đường thẳng d . chỉ sử dụng êke , hãy vẽ đường thẳng d đi qua O và vuông góc với d . nói rõ cách vẽ13 . cho đoạn thẳng AB dài 24mm . hãy vẽ đường trung trực của đoạn thẳng ấy . nói rõ cách vẽ Chú ý : các bạn khỏi vẽ hình , chỉ cần giúp mik nói rõ cách vẽ là ok rồi cảm ơn nhìu , giải giúp mik trước 8 h...
Đọc tiếp
11. cho đường thẳng d và điểm O thuộc d . vẽ đường thẳng d' đi qua O và vuông góc với d . nói rõ cách vẽ và cách sử dụng công cụ ( êke , thước kẻ ) để vẽ .
12. cho đường thẳng d và điểm O nằm ngoài đường thẳng d . chỉ sử dụng êke , hãy vẽ đường thẳng d' đi qua O và vuông góc với d . nói rõ cách vẽ
13 . cho đoạn thẳng AB dài 24mm . hãy vẽ đường trung trực của đoạn thẳng ấy . nói rõ cách vẽ
Chú ý : các bạn khỏi vẽ hình , chỉ cần giúp mik nói rõ cách vẽ là ok rồi cảm ơn nhìu , giải giúp mik trước 8 h nha
Cho đường thẳng d và điểm O nằm ngoài đường thẳng d. Chỉ sử dụng eke, hãy vẽ đường thẳng d' đi qua O và vuông góc với d. Nói rõ cách vẽ.
(Nói cách vẽ là được rồi, ko cần vẽ hình đâu)
Cho đường thẳng d và điểm O thuộc d. Vẽ đường thẳng d’ đi qua O vuông góc với d. Nói rõ cách vẽ và cách sử dụng công cụ (êke, thước thẳng) để vẽ.
(( Không cần vẽ hình nha))
- Dùng thước thẳng vẽ d
- Lấy điểm O trên d
- Dùng êke vẽ d' vuông góc với d tại O
- Dùng thước thẳng vẽ d
- Lấy điểm O ngoài d
- Dùng êke vẽ d' qua O vuông góc với d
Đúng 0
Bình luận (0)
#)Trả lời :
- Đặt cạnh thước thẳng theo đường thẳng d.
- Đặt cạnh góc vuông của êke trùng với đường thẳng d sao cho đỉnh góc vuông êke trùng điểm O.
- Kẻ đường thẳng đi qua cạnh góc vuông thứ hai ta được đường thẳng d’ vuông góc với d tại O.
Đúng 0
Bình luận (0)

giải, trình bày rõ ràng đầy đủ và vẽ hình giúp mình với ạ mình cảm ơn
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
Đúng 0
Bình luận (0)