Chứng minh rằng với mọi số nguyên a ta có:
a.(a+1)+1>0
Chứng minh rằng với mọi a ,ta có:
a,(a - 4)(a+2)+6 ko là bội của 9
Chứng minh rằng với mọi góc \(\alpha \;\;({0^o} \le \alpha \le {180^o})\), ta đều có:
a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
b) \(\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})\)
c) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})\)
d) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})\)
a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
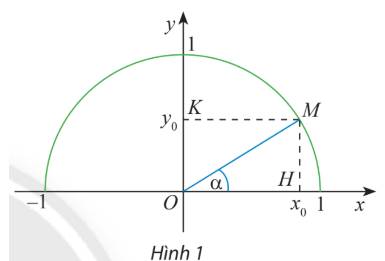
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)
Chứng minh rằng với mọi số thực a, b ta luôn có:
a)\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
b)\(a^2+b^2+c^2\ge ab+bc+ca\)
`a) 2 ( a^2 + b^2 ) >= ( a + b )^2`
`<=> 2a^2 + 2b^2 >= a^2 + 2ab + b^2`
`<=> a^2 - 2ab + b^2 >= 0`
`<=> ( a - b )^2 >= 0` (Luôn đúng `AA a,b`)
`=>` Đẳng thức được c/m
_________________________________________
`b) a^2 + b^2 + c^2 >= ab + bc + ca`
`<=> 2a^2 + 2b^2 + 2c^2 >= 2ab + 2bc + 2ca`
`<=> ( a^2 - 2ab + b^2 ) + ( b^2 - 2bc + c^2 ) + ( c^2 - 2ca + a^2 ) >= 0`
`<=> ( a - b )^2 + ( b - c )^2 + ( c - a )^2 >= 0` (Luôn đúng `AA a,b,c`)
`=>` Đẳng thức được c/m
chứng minh rằng với mọi số a ta có a.(a+1)+1>0
Ta có a(a + 1) + 1 = a2 + a + 1 = \(a^2+2.\frac{1}{2}a+\frac{1}{4}+\frac{3}{4}=\left(a+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)(đpcm)
Chứng minh với mọi a,b ta có:a^2+b^2+4>=ab+2(a+b)
\(a^2+b^2+4\ge ab+2\left(a+b\right)\)
\(\Leftrightarrow2a^2+2b^2+8\ge2ab+4\left(a+b\right)\)
\(\Leftrightarrow2a^2+2b^2+8-2ab-4a-4b\ge0\)
\(\Leftrightarrow a^2-2ab+b^2+a^2-4a+4+b^2-4b+4\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-2\right)^2+\left(b-2\right)^2\ge0\) (Luôn đúng)
Vậy đẳng thức ban đầu được chứng minh.
chứng minh rằng với mọi số a, ta có :\(\dfrac{a^2+a+1}{a^2-a+1}>0\)
\(\dfrac{a^2+a+1}{a^2-a+1}=\dfrac{a^2+2.a.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}}{a^2-2.a.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}}\)
\(=\dfrac{\left(a+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}{\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}>0\) ( luôn đúng)
Chứng minh rằng với mọi số nguyên a khác 0 và a khác -1 thì 2a+1/ 2a2+2a là phân số tối giản.
ta có: \(\frac{2a+1}{2a^2+2a}=\frac{2a+1}{2a\left(a+1\right)}\)
nhận xét: 2a và 2a +1 là 2 số nguyên liên tiếp nên 2a và 2a + 1 không có ước chung nào khác 1; -1 (*)
gọi d = ƯCLN(2a+1; a+1)
=> 2a+1 chia hết cho d và
a+ 1 chia hết cho d
=> 2a+ 1 - 2(a+1) = -1 chia hết cho d => d = 1 hoặc -1 => 2a+ 1 và a+ 1 nguyên tố cùng nhau hay chúng ko có ước chung nào khác 1; -1 (**)
Từ (*)(**) => 2a + 1 và 2a.(a+ 1) nguyên tố cùng nhau => phân số đã cho là tối giản
chứng minh rằng với mọi số a, ta có:
\(\frac{a^2+a+1}{a^2-a+1}>0\)
Ta có: \(a^2+a+1=a^2+a+\frac{1}{4}+\frac{3}{4}=\left(a+\frac{1}{2}\right)^2+\frac{3}{4}>0\)
\(a^2-a+1=a^2-a+\frac{1}{4}+\frac{3}{4}=\left(a-\frac{1}{2}\right)^2+\frac{3}{4}>0\)
\(\Rightarrow\frac{a^2+a+1}{a^2-a+1}>0\forall a\in R\)
Chứng minh rằng với mọi tam giác ABC ta có:
a) \(SinA+SinB+SinC\le Cos\dfrac{A}{2}+Cos\dfrac{B}{2}+Cos\dfrac{C}{2}\)
b) \(CosA.CosB.CosC\le Sin\dfrac{A}{2}.Sin\dfrac{B}{2}.Sin\dfrac{C}{2}\)