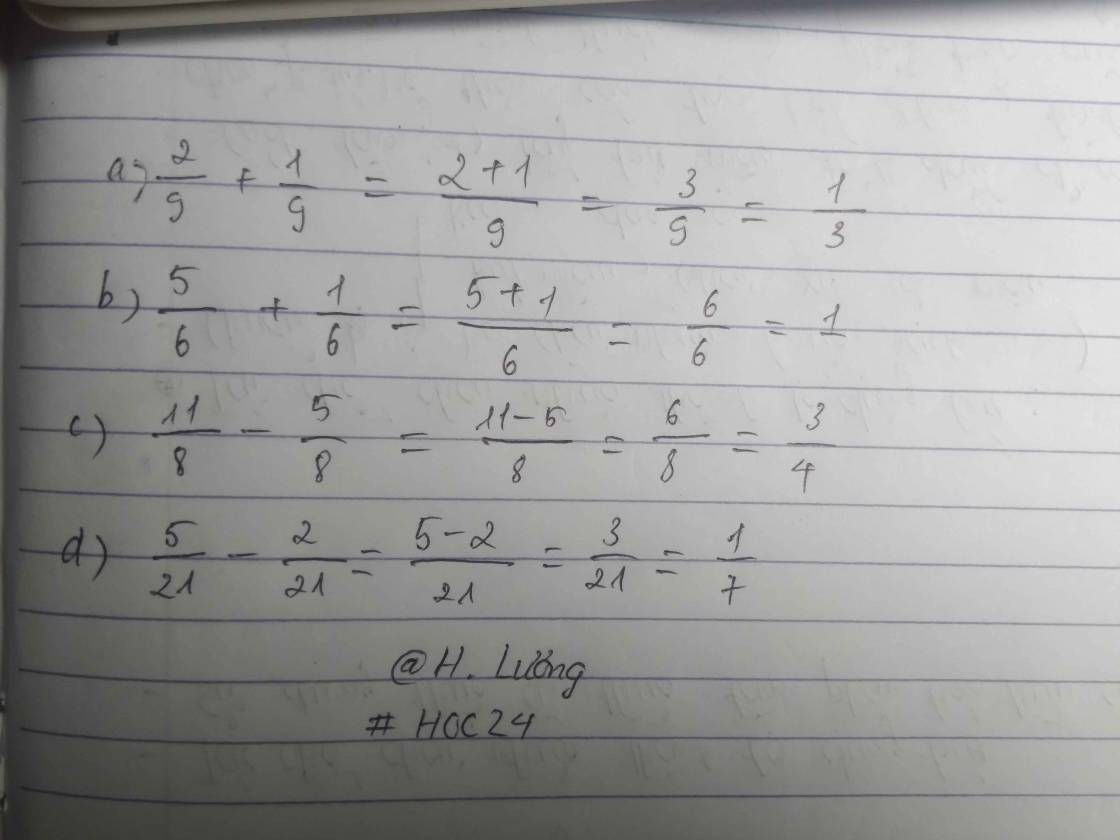Rút gọn:A=1+5+5^2+5^3+...5^2008+5^200
BH
Những câu hỏi liên quan
Rút Gọn:
a) (2x+5)3-(2x-5)3-(120x2+49)
b) (4-5x)2 - (3+5x)2
a) `(2x+5)^3-(2x-5)^3-(120x^2+49)`
`=(2x+5-2x+5)[(2x+5)^2+(2x+5)(2x-5)+(2x-5)^2]-(120x^2+49)`
`=10(12x^2+25)-(120x^2+49)`
`=120x^2+250-120x^2-49`
`=201`
b) `(4-5x)^2-(3+5x)^2=(4-5x+3+5x)(4-5x-3-5x)=7.(-10x+1)=-70x+7`
Đúng 3
Bình luận (0)
Lời giải:
a.
$(2x+5)^3-(2x-5)^3-(120x^2+49)$
$=[(2x+5)-(2x-5)][(2x+5)^2+(2x+5)(2x-5)+(2x-5)^2]-(120x^2+49)$
$=10(4x^2+20x+25+4x^2-25+4x^2-20x+25)-(120x^2+49)$
$=10(12x^2+25)-(120x^2+49)=250-49=201$
b.
$(4-5x)^2-(3+5x)^2=[(4-5x)+(3+5x)][(4-5x)-(3+5x)]$
$=7(1-10x)$
Đúng 4
Bình luận (0)
a) Ta có: \(\left(2x+5\right)^3-\left(2x-5\right)^3-\left(120x^2+49\right)\)
\(=8x^3+60x^2+150x+125-8x^3+60x^2-150x+125-120x^2-49\)
\(=201\)
b) Ta có: \(\left(4-5x\right)^2-\left(3+5x\right)^2\)
\(=\left(4-5x-3-5x\right)\left(4-5x+3+5x\right)\)
\(=7\left(-10x+1\right)\)
\(=-70x+7\)
Đúng 1
Bình luận (0)
1. Tính : \(\dfrac{12}{4-\sqrt{10}}\)-6\(\sqrt{\dfrac{5}{2}}\)+\(\dfrac{5\sqrt{2}+\sqrt{10}}{\sqrt{5}+1}\)
2,Rút gọn:A=(\(\dfrac{\sqrt{x}}{\sqrt{x}-5}\)-\(\dfrac{5}{\sqrt{x}+5}\)+\(\dfrac{10\sqrt{x}}{25-x}\)):\(\dfrac{3}{\sqrt{x}+5}\)
1: \(=8+2\sqrt{10}-3\sqrt{10}+\sqrt{10}=8\)
Đúng 0
Bình luận (0)
Rút gọn:a)dfrac{5sqrt{2}-2sqrt{5}}{sqrt{5}-sqrt{2}}+dfrac{6}{2-sqrt{10}}b)dfrac{6}{sqrt{5}-1}+dfrac{7}{1-sqrt{3}}-dfrac{2}{sqrt{3}-sqrt{5}}c)left(dfrac{sqrt{14}-sqrt{7}}{1-sqrt{2}}+dfrac{sqrt{15}-sqrt{5}}{1-sqrt{3}}right)divdfrac{1}{sqrt{7}-sqrt{5}}d)sqrt{2}+dfrac{1}{sqrt{5+2sqrt{6}}}+dfrac{2}{sqrt{8+2sqrt{15}}}e)left(dfrac{15}{sqrt{6}+1}+dfrac{4}{sqrt{6}-2}-dfrac{12}{3-sqrt{6}}right)timesleft(sqrt{6}+11right)Lm nhanh giúp mk nhé, mk đang cần gấp!
Đọc tiếp
Rút gọn:
a)\(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{5}-\sqrt{2}}+\dfrac{6}{2-\sqrt{10}}\)
b)\(\dfrac{6}{\sqrt{5}-1}+\dfrac{7}{1-\sqrt{3}}-\dfrac{2}{\sqrt{3}-\sqrt{5}}\)
c)\(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right)\div\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
d)\(\sqrt{2}+\dfrac{1}{\sqrt{5+2\sqrt{6}}}+\dfrac{2}{\sqrt{8+2\sqrt{15}}}\)
e)\(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\times\left(\sqrt{6}+11\right)\)
Lm nhanh giúp mk nhé, mk đang cần gấp!
Bạn chia nhỏ ra để nhận được câu tl sớm nhất nhé!Bạn đặt câu hỏi free mà để dày cộp như này khum ai dám làm =(((
Đúng 0
Bình luận (0)
1,Tính \(\dfrac{12}{4-\sqrt{10}}-6\sqrt{\dfrac{5}{2}}+\dfrac{5\sqrt{2}+\sqrt{10}}{\sqrt{5}+1}\)
2,Rút gọn:A=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{5}{\sqrt{x}+5}+\dfrac{10\sqrt{x}}{25-x}\right):\dfrac{3}{\sqrt{x}+5}\)
1: \(=8+2\sqrt{10}-3\sqrt{10}+\sqrt{10}=8\)
Đúng 0
Bình luận (1)
Rút gọn:
A=\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}\)
B=\(\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}\)
\(B=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}\)
\(B=\sqrt{\left(\sqrt{5}+2\right)^2}+\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(B=\left|\sqrt{5}+2\right|+\left|\sqrt{5}-2\right|\)
\(B=\sqrt{5}+2+\sqrt{5}-2\)
\(B=2\sqrt{5}\)
Đúng 1
Bình luận (4)
\(A=\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}\)
\(A=\left(\dfrac{\sqrt{12}-\sqrt{6}}{2\sqrt{2}-2}-\dfrac{6\sqrt{6}}{3}\right).\dfrac{1}{\sqrt{6}}\)
\(A=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-2\sqrt{6}\right).\dfrac{1}{\sqrt{6}}\)
\(A=\left(\sqrt{6}-2\sqrt{6}\right).\dfrac{1}{\sqrt{6}}\)
\(A=-\sqrt{6}.\dfrac{1}{\sqrt{6}}\)
\(A=-1\)
Đúng 2
Bình luận (1)
Rút gọn:
A= \(\sqrt{6-2\sqrt{5}}\) C= \(\sqrt{19-8\sqrt{3}}\)
B = \(\sqrt{4-\sqrt{12}}\) D= \(\sqrt{5-2\sqrt{6}}\)
`A=\sqrt{6-2\sqrt{5}}`
`A=\sqrt{(\sqrt{5}-1)^2}`
`A=\sqrt{5}-1`
_________
`B=\sqrt{4-\sqrt{12}}=\sqrt{4-2\sqrt{3}}`
`B=\sqrt{(\sqrt{3}-1)^2}`
`B=\sqrt{3}-1`
_________
`C=\sqrt{19-8\sqrt{3}}`
`C=\sqrt{(4-\sqrt{3})^2}`
`C=4-\sqrt{3}`
_________
`D=\sqrt{5-2\sqrt{6}}`
`D=\sqrt{(\sqrt{3}-\sqrt{2})^2}`
`D=\sqrt{3}-\sqrt{2}`
Đúng 2
Bình luận (1)
\(A=\sqrt{6-2\sqrt{5}}=\sqrt{\sqrt{5}^2-2\sqrt{5}+1^2}=\sqrt{ \left(\sqrt{5}-1\right)^2}=\sqrt{5}-1\)
\(B=\sqrt{4-\sqrt{12}}=\sqrt{4-\sqrt{4.3}}=\sqrt{4-2\sqrt{3}}=\sqrt{\sqrt{3^2}-2\sqrt{3}+1^2}=\sqrt{\left(\sqrt{3}-1\right)^2}=\sqrt{3}-1\)
\(C=\sqrt{19-8\sqrt{3}}=\sqrt{19-2.4.\sqrt{3}}\sqrt{\sqrt{3}^2-2.4.\sqrt{3}+4^2}=\sqrt{\left(\sqrt{3}-4\right)^2}=\sqrt{3}-4\)
\(D=\sqrt{5-2\sqrt{6}}=\sqrt{5-2.\sqrt{2}.\sqrt{3}}=\sqrt{\sqrt{3}^2-2.\sqrt{2}.\sqrt{3}+\sqrt{2^2}}=\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}=\sqrt{3}-\sqrt{2}\)
Đúng 0
Bình luận (1)
Tính rồi rút gọn:
a) \(\dfrac{2}{9}+\dfrac{1}{9}\) b) \(\dfrac{5}{6}+\dfrac{1}{6}\) c) \(\dfrac{11}{8}-\dfrac{5}{8}\) d) \(\dfrac{5}{21}-\dfrac{2}{21}\)
Rút gọn:a) 2sqrt{98}-3sqrt{18}+dfrac{1}{2}sqrt{32}b)left(5sqrt{2}+2sqrt{5}right).sqrt{5}-sqrt{250}c)left(2sqrt{3}-5sqrt{2}right).sqrt{3}-sqrt{36}d)3sqrt{48}+2sqrt{27}-dfrac{1}{3}sqrt{243}e) 6sqrt{dfrac{1}{3}}+dfrac{9}{sqrt{3}}-dfrac{2}{sqrt{3}-1}f)4sqrt{dfrac{1}{2}}-dfrac{6}{sqrt{2}}dfrac{2}{sqrt{2}+1}
Đọc tiếp
Rút gọn:
a) \(2\sqrt{98}-3\sqrt{18}+\dfrac{1}{2}\sqrt{32}\)
b)\(\left(5\sqrt{2}+2\sqrt{5}\right).\sqrt{5}-\sqrt{250}\)
c)\(\left(2\sqrt{3}-5\sqrt{2}\right).\sqrt{3}-\sqrt{36}\)
d)\(3\sqrt{48}+2\sqrt{27}-\dfrac{1}{3}\sqrt{243}\)
e) \(6\sqrt{\dfrac{1}{3}}+\dfrac{9}{\sqrt{3}}-\dfrac{2}{\sqrt{3}-1}\)
f)\(4\sqrt{\dfrac{1}{2}}-\dfrac{6}{\sqrt{2}}\dfrac{2}{\sqrt{2}+1}\)
a) \(2\sqrt{98}-3\sqrt{18}+\dfrac{1}{2}\sqrt{32}=14\sqrt{2}-9\sqrt{2}+2\sqrt{2}=7\sqrt{2}\)
b) \(\left(5\sqrt{2}+2\sqrt{5}\right).\sqrt{5}-\sqrt{250}=5\sqrt{10}+10-5\sqrt{10}=10\)
c) \(\left(2\sqrt{3}-5\sqrt{2}\right).\sqrt{3}-\sqrt{36}=6-5\sqrt{6}-6=5\sqrt{6}\)
d) \(3\sqrt{48}+2\sqrt{27}-\dfrac{1}{3}\sqrt{243}=12\sqrt{3}+6\sqrt{3}-3\sqrt{3}=15\sqrt{3}\)
e) \(6\sqrt{\dfrac{1}{3}}+\dfrac{9}{\sqrt{3}}-\dfrac{2}{\sqrt{3}-1}=2\sqrt{3}+3\sqrt{3}=\left(\sqrt{3}+1\right)=4\sqrt{3}-1\)
f) \(4\sqrt{\dfrac{1}{2}}-\dfrac{6}{\sqrt{2}}.\dfrac{2}{\sqrt{2}+1}=2\sqrt{2}-\left(12-6\sqrt{2}\right)=8\sqrt{2}-12\)
Đúng 0
Bình luận (0)
Rút gọn:
a) A=(5-2x)2-4x(x-5)
b) B= (4-3x)(4+3x)+(3x+1)2
c) C= (x+1)3-x(x2+3x+3)
d) D=(2021x-2020)2-2(2021x-2020)(2020x-2021)+(2020x-2021)
a: \(A=\left(2x-5\right)^2-4x\left(x-5\right)\)
\(=4x^2-20x+25-4x^2+20x\)
=25
b: \(B=\left(4-3x\right)\left(4+3x\right)+\left(3x+1\right)^2\)
\(=16-9x^2+9x^2+6x+1\)
=6x+17
c: \(C=\left(x+1\right)^3-x\left(x^2+3x+3\right)\)
\(=x^3+3x^2+3x+1-x^3-3x^2-3x\)
=1
d: \(D=\left(2021x-2020\right)^2-2\left(2021x-2020\right)\left(2020x-2021\right)+\left(2020x-2021\right)^2\)
\(=\left(2021x-2020-2020x+2021\right)^2\)
\(=\left(x+1\right)^2\)
\(=x^2+2x+1\)
Đúng 0
Bình luận (0)