Giúp em câu 2 vs ạ. Vẽ hình hộ
LL
Những câu hỏi liên quan
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
mng giải giúp mik vs ạ, vẽ hộ cả hình với
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
Ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM
Đúng 1
Bình luận (0)
xin lỗi vì đã lm phiền mn ạ, giải hộ em với, em lm hết a với b rồi nên a chị nào giúp em câu c và d với ạ, đc sử dụng dữ kiện của câu trên nhé. GT ( đề bài ) ở bên phải hình vẽ ạ. HTC là hình thag cân ạ, còn cái (n) trong GT là cắt >< Mong mn giúp e ạ
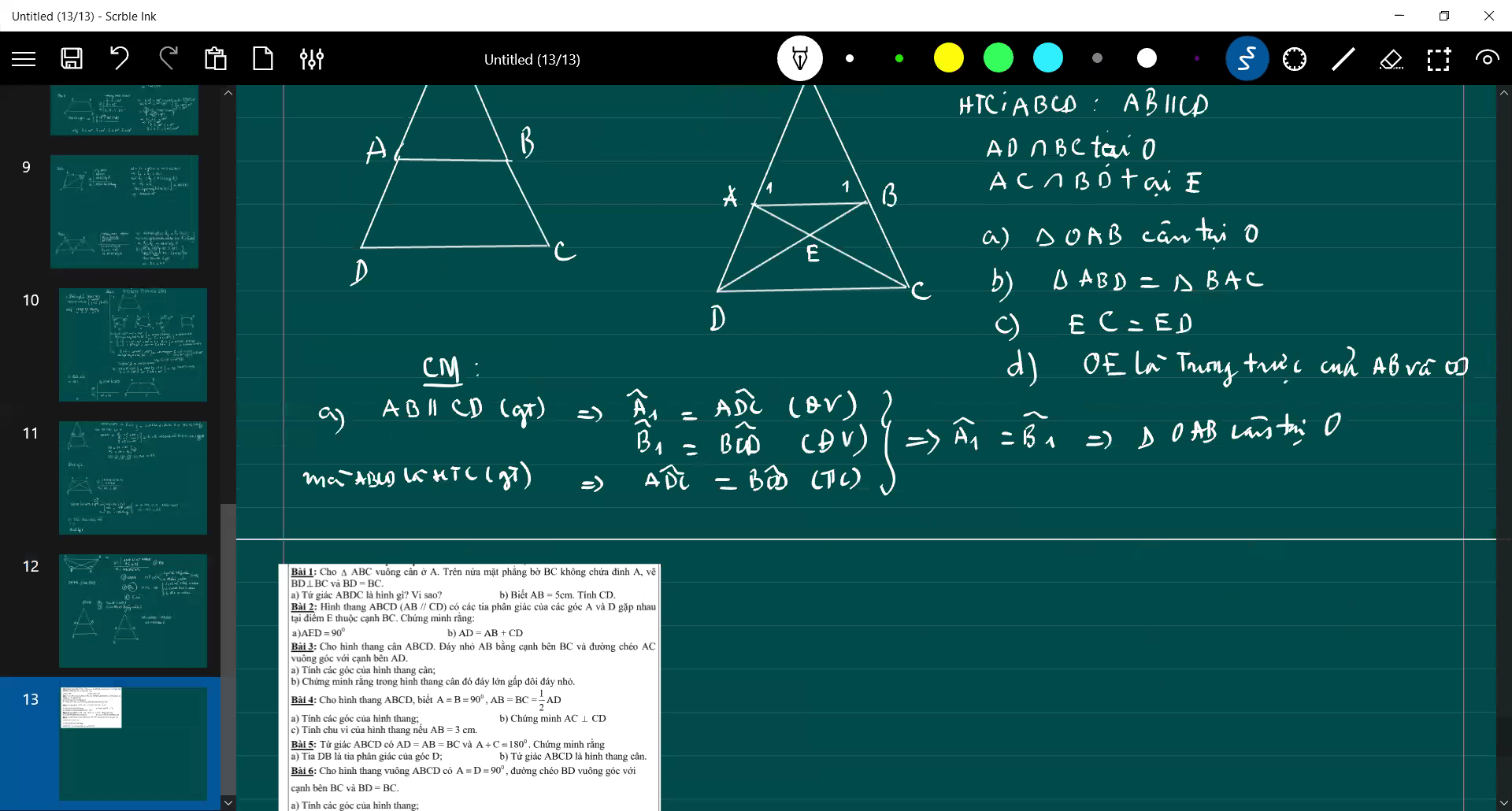
có j thắc mắc thì mn cứ hỏi ạ, em cần trc sáng mai nhé!? ><
Đúng 0
Bình luận (0)
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
Đúng 0
Bình luận (0)
Anh chị ơi giúp e câu toán hình 9 với mai e thi rồi.Em cản ơn rất nhiều ạ.( vẽ hình hộ em nha)❤❤❤❤
Gọi xy là tiếp tuyến tại A của (O)
=>góc xAC=góc ABC
xy//DE
=>góc xAE=góc AED
=>góc AED=góc ABC
Xét ΔAED và ΔABC có
góc AED=góc ABC
góc EAD chung
=>ΔAED đồng dạng với ΔABC
=>AE/AB=AD/AC
=>AE*AC=AB*AD
Đúng 0
Bình luận (0)
Hộ câu 2 giúp em. Ko cần vẽ hình nữa. Em camon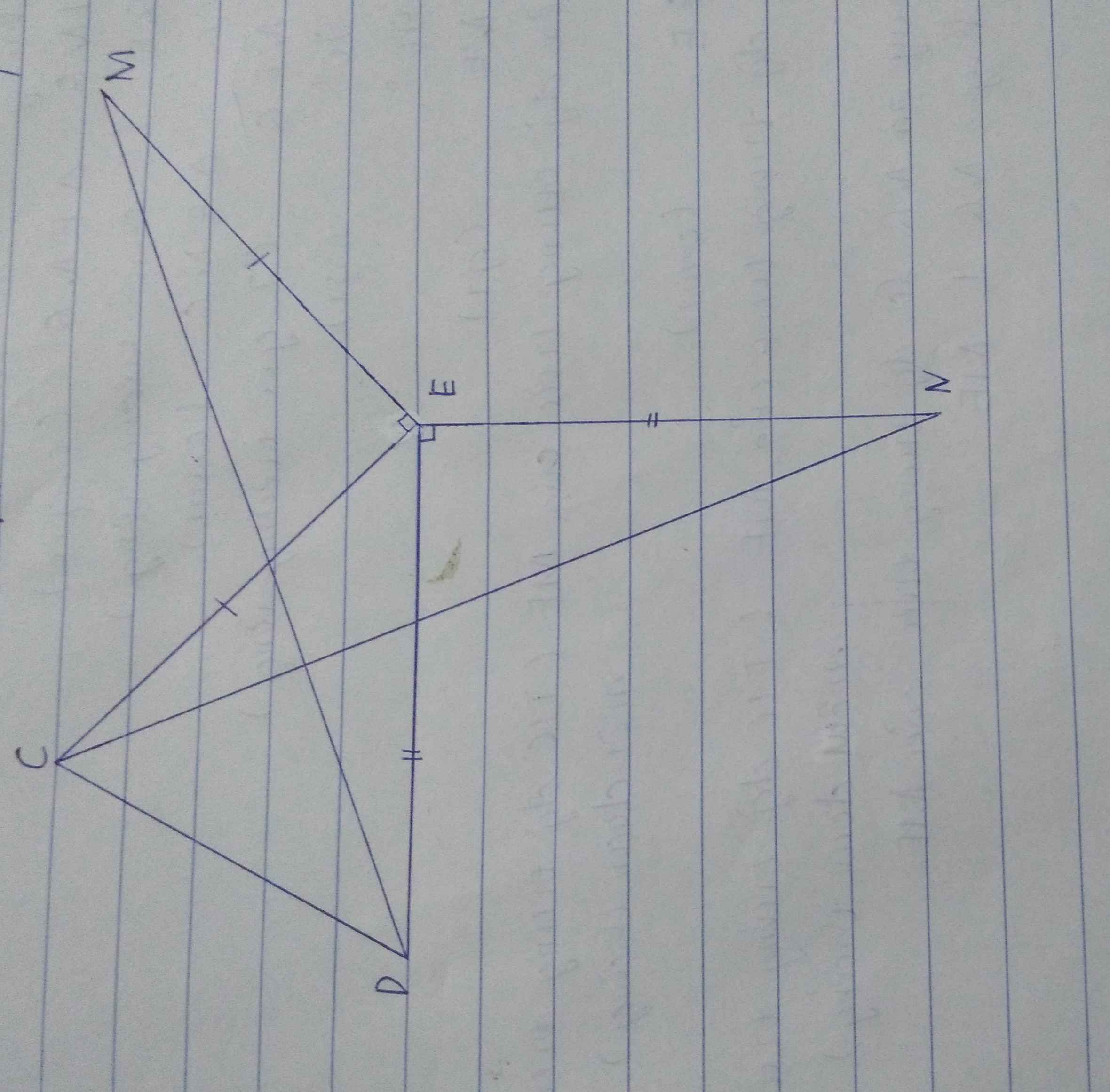

a) Dễ dàng c/m đc tam giác MED = tam giác CEN
=> MD = CN (2 cạnh tương ứng)
b) Gọi O là giao điểm của CE và DM
Tam giác MED = tam giác CEN
=> Góc EMD = Góc ECN (2 góc tương ứng)
Mà: \(\left\{{}\begin{matrix}\widehat{EOM}=\widehat{COD}\left(đối-đỉnh\right)\\\widehat{EOM}+\widehat{EMD}=90^0\end{matrix}\right.\)
=> Góc ECN + Góc COD = 90o
=> Góc COM = 90o
=> MD vuông góc CN
Đúng 2
Bình luận (0)
a) Ta chứng minh đc tam giác MED = tam giác CEN
=> MD = CN (2 cạnh tương ứng)
b) Gọi O là giao điểm của CE và DM
Tam giác MED = tam giác CEN
=> Góc EMD = Góc ECN (2 góc tương ứng)
Mà: {ˆEOM=ˆCOD(đối−đỉnh)ˆEOM+ˆEMD=900{EOM^=COD^(đối−đỉnh)EOM^+EMD^=900
=> Góc ECN + Góc COD = 90o
=> Góc COM = 90o
=> MD vuông góc CN
Đúng 0
Bình luận (0)
Cho Hình chữ nhật ABCD có AB=8cm , AD =6cm . KẺ AH vuông góc vs BD tại H . tTính BD , AH , BH , CH , DH( vẽ hÌNH HỘ MK NỮA NHÉ0
.. em đg cần gấp mong m.n giúp e vs ạ..e xjn cảm ơn
Vẽ giúp e hình câu a vs ạ

Giúp em vẽ hình vs ạ
a: Xét ΔBAM và ΔBDM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔBAM=ΔBDM
Suy ra: \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
b: Xét ΔMAH vuông tại A và ΔMDC vuông tại D có
MA=MD
\(\widehat{AMH}=\widehat{DMC}\)
Do đó: ΔMAH=ΔMDC
c: Ta có: ΔBAM=ΔBDM
nên MA=MD
mà MD<MC
nên MA<MC
d: Ta có: BH=BC
nên B nằm trên đường trung trực của CH(1)
Ta có; MH=MC
nên M nằm trên đường trung trực của CH(2)
Ta có: KH=KC
nên K nằm trên đường trung trực của CH(3)
Từ (1), (2) và (3) suy ra B,M,K thẳng hàng
Đúng 2
Bình luận (1)
Làm giúp em câu d vs ạ. Vẽ sơ đồ khối ra thôi ạ
uses crt;
var a:array[1..100] of integer;
i,n,d,tong :integer;
begin
clrscr;
d:=0;
tong:=0;
readln(n);
for i:=1 to n do
readln(a[i]);
end;
for i:=1 to n do
if (a[i]>0) then begin
d:=d+1;
if d=1 then begin writeln('trong day co so nguyen duong '); write(' vi tri cua cac so duong ',i); end
else
begin
tong:=tong+a[i];
write(' ',i);
end;
end
else if ((i=n)and(d=0)) then write(' khong co so duong');
writeln;
writeln(' tong so luong so nguyen duong trong day so: ',d);
writeln(' ton cac so nguyen duong: ',tong);
readln;
end.
Đúng 0
Bình luận (0)





