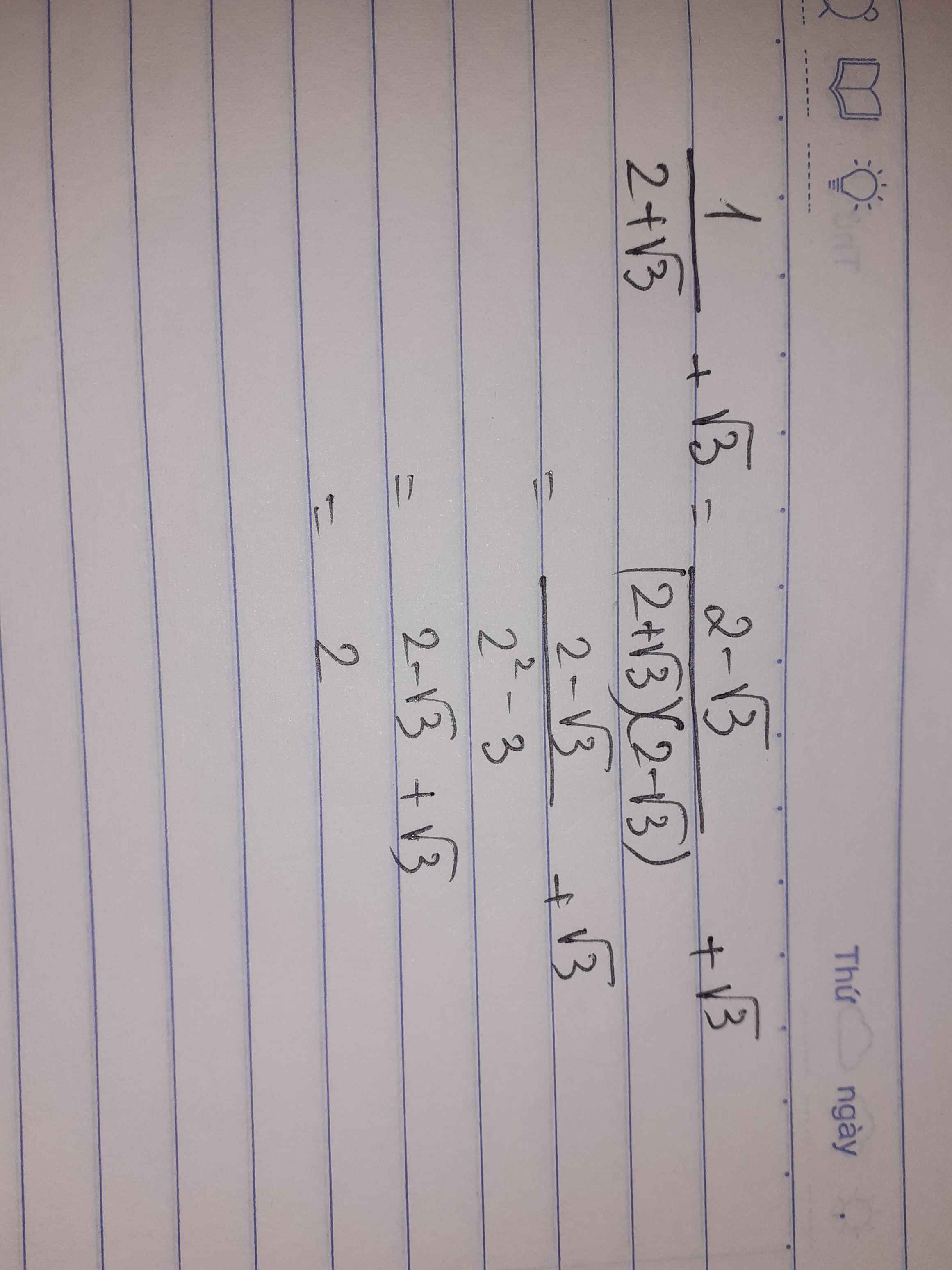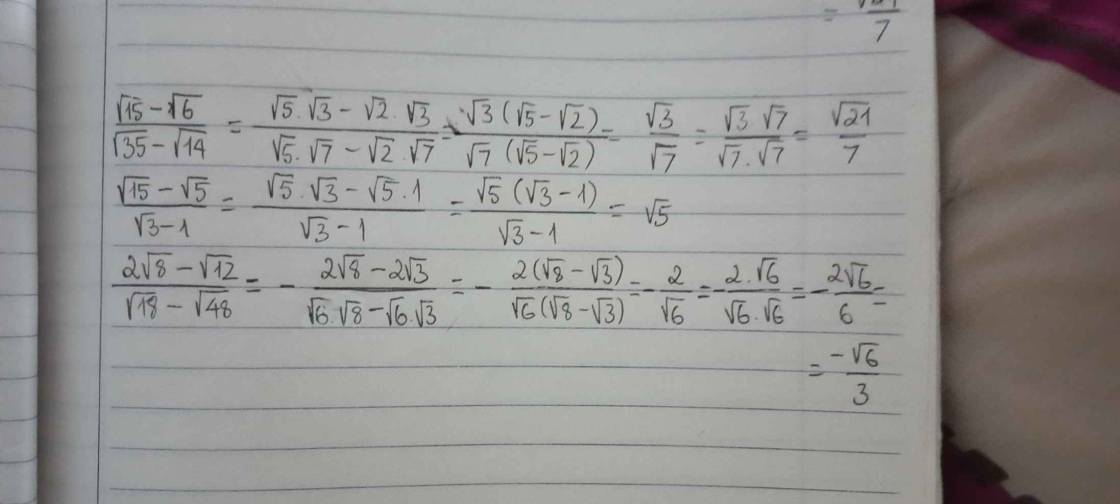rút gọn bt sau \(\dfrac{\sqrt{8-2\sqrt{12}}}{\sqrt{3}-1}\)
TT
Những câu hỏi liên quan
Rút gọn bt sau \(\dfrac{1}{2+\sqrt{3}}+\sqrt{3}\)
Ta có: \(\dfrac{1}{2+\sqrt{3}}+\sqrt{3}\)
\(=2-\sqrt{3}+\sqrt{3}\)
=2
Đúng 0
Bình luận (0)
rút gọn bt sau \(\dfrac{2\sqrt{3}}{\sqrt{3+\sqrt{2}}}+\sqrt{24}\)
Ta có: \(\dfrac{2\sqrt{3}}{\sqrt{3}+\sqrt{2}}+\sqrt{24}\)
\(=2\sqrt{3}\left(\sqrt{3}-\sqrt{2}\right)+2\sqrt{6}\)
\(=6-2\sqrt{6}+2\sqrt{6}\)
=6
Đúng 3
Bình luận (0)
a) tính gtrị của biểu thức A = \(\sqrt{3}+\sqrt{12}-\sqrt{27}-\sqrt{36}\)
b) cho bt B = \(\dfrac{2}{\sqrt{x-1}}-\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x-5}}{\sqrt{x\left(\sqrt{x-1}\right)}}\) với x > 0 và x \(\ne\) 1 . rút gọn bt và tìm x để B = 2
\(a,\) ta có :
\(\Leftrightarrow\left\{{}\begin{matrix}A=\sqrt{3}+\sqrt{2^2.3}-\sqrt{3^2.3}-\sqrt{6^2}\\A=\sqrt{3}+2\sqrt{3}-3\sqrt{3}-6\\A=\sqrt{3}.\left(1+2-3\right)-6\\A=-6\end{matrix}\right.\)
\(\Rightarrow A=-6\) . vậy \(A=9\sqrt{5}\)
__________________________________________________________
\(b,\) với \(x>0\) và \(x\ne1\) . ta có :
\(B=\dfrac{2}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{2\sqrt{x}-\left(\sqrt{x}-1\right)+3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{2\sqrt{x}-\sqrt{x}+1+3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\) \(B=\dfrac{4\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{4}{\sqrt{x}}\)
vậy với \(x>0\) \(;\) \(x\ne1\) thì \(B=\dfrac{4}{\sqrt{x}}\)
để \(B=2\) thì \(\dfrac{4}{\sqrt{x}}=2\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\left(tm\right)\)
vậy để \(B=2\) thì \(x=4\)
Đúng 4
Bình luận (1)
* Rút gọn biểu thức
a. \(\sqrt{72}-5\sqrt{2}+3\sqrt{12}\)
b. \(6\sqrt{\dfrac{1}{2}}-\dfrac{2}{\sqrt{2}}-5\sqrt{2}\)
c. \(\dfrac{\sqrt{8}-2}{\sqrt{2}-1}+\dfrac{2}{\sqrt{3}-1}-\dfrac{3}{\sqrt{3}}\)
d. \(\sqrt[3]{64}+\sqrt[3]{27}-2\sqrt[3]{-8}\)
\(a.\sqrt{72}-5\sqrt{2}+3\sqrt{12}\\ =6\sqrt{2}-5\sqrt{2}+6\sqrt{3}\\ =\sqrt{2}+6\sqrt{3}\\ b.6\sqrt{\dfrac{1}{2}}-\dfrac{2}{\sqrt{2}}-5\sqrt{2}\\ =3\sqrt{2}-\sqrt{2}-5\sqrt{2}\\ =-3\sqrt{2}\\ c.\dfrac{\sqrt{8}-2}{\sqrt{2}-1}+\dfrac{2}{\sqrt{3}-1}-\dfrac{3}{\sqrt{3}}\\ =2+1+\sqrt{3}-\sqrt{3}\\ =3\\ d.\sqrt[3]{64}+\sqrt[3]{27}-2\sqrt[3]{-8}\\ =4+3+4\\ =11\)
Đúng 0
Bình luận (0)
rút gọn
\(\dfrac{\sqrt{15}-\sqrt{6}}{\sqrt{35}-\sqrt{14}}\)
\(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}\)
\(\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}\)
\(\dfrac{\sqrt{15}-\sqrt{6}}{\sqrt{35}-\sqrt{14}}=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}=\sqrt{\dfrac{3}{7}}\)
\(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{5}\)
\(\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}=\dfrac{2\left(\sqrt{8}-\sqrt{3}\right)}{\sqrt{6}\left(\sqrt{3}-\sqrt{8}\right)}=-\dfrac{2\sqrt{6}}{6}\)
Đúng 2
Bình luận (0)
`(sqrt 15 - sqrt 6)/(sqrt 35 - sqrt 14)`
`= (sqrt 3 . (sqrt 5 - sqrt 2))/(sqrt 7. (sqrt 5 - sqrt 2))`
`= sqrt3/sqrt 7`
`@ (sqrt 15 - sqrt 5)/(sqrt 3 - 1)`
`= (sqrt 5(sqrt 3 - 1))/(sqrt 3 - 1)`
`= sqrt5`
`@ (2 sqrt 8 - sqrt 12)/(sqrt18 - sqrt 48)`
`= (2(sqrt 8 - sqrt 3)/(sqrt 6(sqrt 3 - sqrt 8))`
`= (-2)/(sqrt 6) = (-2 sqrt 6)/6`
Đúng 2
Bình luận (0)
* Rút gọn các biểu thức
a. \(\sqrt{72}-5\sqrt{2}+3\sqrt{12}\)
b. \(6\sqrt{\dfrac{1}{2}}-\dfrac{2}{\sqrt{2}}-5\sqrt{2}\)
c. \(\dfrac{\sqrt{8}-2}{\sqrt{2}-1}+\dfrac{2}{\sqrt{3}-1}-\dfrac{3}{\sqrt{3}}\)
d. \(\sqrt[3]{64}+\sqrt[3]{27}-2\sqrt[3]{-8}\)
* Rút gọn các biểu thức
a. \(\sqrt{72}-5\sqrt{2}+3\sqrt{12}\)
b. \(6\sqrt{\dfrac{1}{2}}-\dfrac{2}{\sqrt{2}}-5\sqrt{2}\)
c. \(\dfrac{\sqrt{8}-2}{\sqrt{2}-1}+\dfrac{2}{\sqrt{3}-1}-\dfrac{3}{\sqrt{3}}\)
d. \(\sqrt[3]{64}+\sqrt[3]{27}-2\sqrt[3]{-8}\)
Rút gọn biểu thức sau :
\(N=1+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3+\sqrt{8}}}+...+\dfrac{1}{\sqrt{2017+\sqrt{2017^2-1}}}\)
Rút gọn bt A=\(\left(\dfrac{1+\sqrt{x}}{x+1}-\dfrac{4-3\sqrt{x}}{x-4\sqrt{x}+4}\right):\left(\dfrac{x-\sqrt{x}}{x\sqrt{x}-2x+\sqrt{x}-2}\right)\)
Sau đó tìm x để A>1
Ta có: \(A=\left(\dfrac{\sqrt{x}+1}{x+1}-\dfrac{4-3\sqrt{x}}{x-4\sqrt{x}+4}\right):\left(\dfrac{x-\sqrt{x}}{x\sqrt{x}-2x+\sqrt{x}-2}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-4\sqrt{x}+4\right)+\left(3\sqrt{x}-4\right)\left(x+1\right)}{\left(x+1\right)\left(\sqrt{x}-2\right)^2}:\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-2\right)\left(x+1\right)}\)
\(=\dfrac{x\sqrt{x}-4x+4\sqrt{x}+x-4\sqrt{x}+4+3x\sqrt{x}+3\sqrt{x}-4x-4}{\left(x+1\right)\left(\sqrt{x}-2\right)^2}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(x+1\right)}{x-\sqrt{x}}\)
\(=\dfrac{4x\sqrt{x}-7x+3\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\cdot\left(4\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4\sqrt{x}-3}{\sqrt{x}-2}\)
Để A>1 thì A-1>0
\(\Leftrightarrow\dfrac{4\sqrt{x}-3-\sqrt{x}+2}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\dfrac{3\sqrt{x}-1}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\sqrt{x}-1\le0\\\sqrt{x}-2>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0< x\le\dfrac{1}{9}\\x>4\end{matrix}\right.\)
Đúng 2
Bình luận (0)