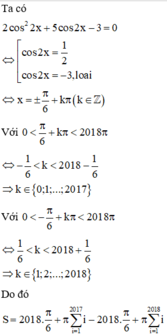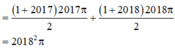2sinxcosx+ 5cos2x -4 = 0
BT
Những câu hỏi liên quan
Giải phương trình sau: 5cos2x + 12sin2x - 13 = 0
Vì  nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn
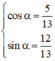
(*) ⇔ cos α.cos 2x + sin α. sin 2x = 1
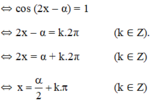
Vậy phương trình có họ nghiệm
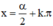 (k ∈ Z)
(k ∈ Z)
với α thỏa mãn 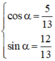
Đúng 0
Bình luận (0)
4sin2x-5cos2x=4
Lời giải:
PT \(\Leftrightarrow \frac{4}{\sqrt{41}}\sin 2x-\frac{5}{\sqrt{41}}\cos 2x=\frac{4}{\sqrt{41}}\)
\(\Leftrightarrow \cos a\sin 2x-\sin a\cos 2x=\frac{4}{\sqrt{41}}\) (với \(a=\arccos \frac{4}{\sqrt{41}}\), \(a\in (0;\frac{1}{2}\pi)\))
\(\Leftrightarrow \sin (2x-a)=\frac{4}{\sqrt{41}}\)
\(\Leftrightarrow x=\frac{1}{2}(\arcsin \frac{4}{\sqrt{41}}+2k\pi +a)\) hoặc \(x=\frac{1}{2}(\pi -\arcsin \frac{4}{\sqrt{41}}+2k\pi +a)\)
Đúng 0
Bình luận (0)
Tổng S các nghiệm của phương trình:
2
c
os
2
2
x
+
5
c
os
2
x
−
3
0
trong khoảng
0
;
2
π
là A.
S
5
π
B.
S
11
π...
Đọc tiếp
Tổng S các nghiệm của phương trình: 2 c os 2 2 x + 5 c os 2 x − 3 = 0 trong khoảng 0 ; 2 π là
A. S = 5 π
B. S = 11 π 6
C. S = 4 π
D. S = 7 π 6
Đáp án C
2 c os 2 2 x + 5 c os 2 x − 3 = 0 ⇔ c os 2 x = 1 2 ; hoặc c os 2 x = − 3 l o a i , c os 2 x = 1 2 ⇔ x = ± π 6 + k π .
Do x ∈ 0 ; 2 π . Vậy tổng các nghiệm của phương trình trong khoảng 0 ; 2 π là: S = π 6 + 7 π 6 + 5 π 6 + 11 π 6 = 4 π
Đúng 0
Bình luận (0)
Tổng S các nghiệm của phương trình:
2
cos
2
2
x
+
5
cos
2
x
-
3
0
trong khoảng
0
;
2
π
là: A.
S
5
π
B.
S
7
π...
Đọc tiếp
Tổng S các nghiệm của phương trình: 2 cos 2 2 x + 5 cos 2 x - 3 = 0 trong khoảng 0 ; 2 π là:
A. S = 5 π
B. S = 7 π 6
C. S = 4 π
D. S = 11 π 6
( 1 + căn 2 ) . ( cosx + sinx ) - 2sinxcosx - 1 - căn2 = 0
Số nghiệm của phương trình sin 2 x + 2 sin x cos x + 3 cos 2 x = 3 thuộc khoảng (0; 2π) là:
A. 1
B. 2
C. 3
D. 4
Chọn C
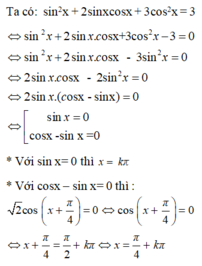
Vậy các nghiệm thuộc khoảng (0, 2π) là π 4 , π , 5 π 4
Đúng 0
Bình luận (0)
Giải phương trình:
a, \(2sin^2x+2sinxcosx-3cos^2x=0\).
b, \(2sin^2x-3sinxcosx+cos^2x=0\).
c, \(2sin^2x-5sinxcosx+3cos^2x=0\).
b) \(2sin^2x-3sinxcosx+cos^2x=0\)
\(\Leftrightarrow2tan^2x-3tanx+1=0\left(cosx\ne0\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=tan\dfrac{\pi}{4}\\tanx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{2}\right)+k\pi\end{matrix}\right.\left(k\in Z\right)\)
Đúng 2
Bình luận (0)
Gọi S là tổng tất cả các nghiệm của phương trình
2
cos
2
2
x
+
5
cos
2
x
-
3
0
trong khoảng
0
;
2018
π
. Tính S. A.
S
1010
.
2018
π
B.
S
2018
2...
Đọc tiếp
Gọi S là tổng tất cả các nghiệm của phương trình 2 cos 2 2 x + 5 cos 2 x - 3 = 0 trong khoảng 0 ; 2018 π . Tính S.
A. S = 1010 . 2018 π
B. S = 2018 2 π
C. S = 2016 . 2018 π
D. S = 2020 . 2018 π
giải dùm mình với 2sinxcosx-(sinx+cosx)+1=0
\(\Leftrightarrow1+2sinx.cosx-\left(sinx+cosx\right)=0\)
\(\Leftrightarrow sin^2x+cos^2x+2sinx.cosx-\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)^2-\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=0\\sin\left(x+\frac{\pi}{4}\right)=\frac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=k\pi\\x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=k2\pi\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)