viết lại đa thức thành vế kia hằng đẳng thức
(x2 + 32)2
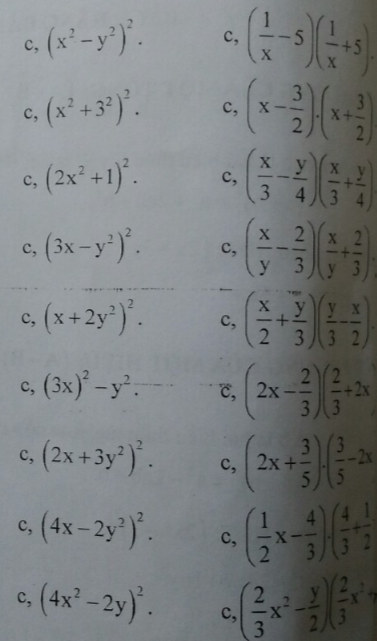 viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
c) \(\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)
c) \(\left(x^2+3^2\right)^2=x^4+18x+81\)
c) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
c) \(\left(3x-y^2\right)^2=9x^2-6xy^2+y^4\)
c) \(\left(x+2y^2\right)^2=x^2+4xy^2+4y^4\)
c) \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
c) \(\left(2x+3y^2\right)^2=4x^2+12xy^2+9y^4\)
c) \(\left(4x-2y^2\right)^2=16x^2-16xy^2+4y^4\)
c) \(\left(4x^2-2y\right)^2=16x^4-16x^2y+4y^2\)
c) \(\left(\dfrac{1}{x}-5\right)\left(\dfrac{1}{x}+5\right)=\dfrac{1}{x^2}-25\)
c) \(\left(x-\dfrac{3}{2}\right)\left(x+\dfrac{3}{2}\right)=x^2-\dfrac{9}{4}\)
c) \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
c) \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
c) \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{y}{3}-\dfrac{x}{2}\right)=\dfrac{y^2}{9}-\dfrac{x^2}{4}\)
c) \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=4x^2-\dfrac{4}{9}\)
c) \(\left(2x+\dfrac{3}{5}\right)\left(\dfrac{3}{5}-2x\right)=\dfrac{9}{25}-4x^2\)
c) \(\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{4}{4}+\dfrac{1}{2}x\right)=\dfrac{1}{4}x^2-\dfrac{16}{9}\)
c) \(\left(\dfrac{2}{3}x^2-\dfrac{y}{2}\right)\left(\dfrac{2}{3}x^2+\dfrac{y}{2}\right)=\dfrac{4}{9}x^4-\dfrac{y^2}{4}\)
Viết lại đa thức thành vế kia hằng đẳng thức
a. (2x - 3y)^2
b (3\(\sqrt{x}\)- y)^2
( 2x - 3y )2 = 4x2 - 12xy + 9y2
( 3√x - y )2 = 9x - 6y√x + y2 ( x ≥ 0 )
2: Viết lại các đa thức thành vế kia hằng đẳng thức:
a, 4x^(4)-4x^(2)+16
b, (x+2y)^(2).
c, 36+x^(2)-12xy
d, (x+5y)^(2).
e, 4x^(2)-12x+9
f,(x-2y)^(2).
\(4x^4-4x^2+1=\left(2x^2-1\right)^2\)
\(\left(x+2y\right)^2=x^2+4xy+4y^2\)
\(36-12x+x^2=\left(6-x\right)^2\)
\(\left(x+5y\right)^2=x^2+10xy+25y^2\)
\(4x^2-12x+9=\left(2x-3\right)^2\)
\(\left(x-2y\right)^2=x^2-4xy+4y^2\)
viết lại đa thức thành vế kia hằng đẳng thức
a/ 36+x^2 - 12x
b/ (x+2y)^2
c/(\(\sqrt{x}\)-2\(\sqrt{y}\))^2
a/ \(36+x^2-12x=x^2-2x.6+6^2=\left(x+6\right)^2\)
b/ \(\left(x+2y\right)^2=x^2+2x.2y+\left(2y\right)^2=x^2+4xy+4y^2\)
c/ \(\left(\sqrt{x}-2\sqrt{y}\right)^2=\left(\sqrt{x}\right)^2-2\sqrt{x}.2\sqrt{y}+\left(2\sqrt{y}\right)^2=x-4\sqrt{xy}+4y\)
viết lại đa thức thành vế kia hằng đẳng thức
a. (\(\frac{x}{y}\)-\(\frac{2}{3}\)) (\(\frac{x}{y}\)+\(\frac{2}{3}\))
b. (2\(\sqrt{x}\) - \(\frac{2}{3}\)) (\(\frac{2}{3}\) + 2\(\sqrt{x}\))
a, \(\left(\frac{x}{y}-\frac{2}{3}\right)\left(\frac{x}{y}+\frac{2}{3}\right)=\left(\frac{x}{y}\right)^2-\left(\frac{2}{3}\right)^2\)
b,\(\left(2\sqrt{x}-\frac{2}{3}\right)\left(\frac{2}{3}+2\sqrt{x}\right)=\left(2\sqrt{x}-\frac{2}{3}\right)\left(2\sqrt{x}+\frac{2}{3}\right)\)
\(=\left(2\sqrt{x}\right)^2-\left(\frac{2}{3}\right)^2\)
Trả lời:
a, \(\left(\frac{x}{y}-\frac{2}{3}\right)\left(\frac{x}{y}+\frac{2}{3}\right)\)\(=\left(\frac{x}{y}\right)^2-\left(\frac{2}{3}\right)^2=\frac{x^2}{y^2}-\frac{4}{9}\)
b, \(\left(2\sqrt{x}-\frac{2}{3}\right)\left(\frac{2}{3}+2\sqrt{x}\right)=\left(2\sqrt{x}-\frac{2}{3}\right)\left(2\sqrt{x}+\frac{2}{3}\right)=\left(2\sqrt{x}\right)^2-\left(\frac{2}{3}\right)^2=4x-\frac{4}{9}\)
viết vế còn lại của hằng đẳng thức
4x^2-20xy^2+25Y^4
\(4x^2-20xy^2+25y^4=\left(2x\right)^2-2.2x.5y^2+\left(5y^2\right)^2=\left(2x-5y^2\right)^2\)
Áp dụng hằng đẳng thức: \(\left(A-B\right)^2=A^2-2AB+B^2\)
\(4x^2-20xy^2+25y^4\)
\(=\left(2x\right)^2-2\cdot2x\cdot5y^2+\left(5y\right)^2\)
\(=\left(2x-5y\right)^2\)
\(4x^2-20xy^2+25y^4\)
\(=\left(2x\right)^2-2.2.5.xy^2+\left(5y\right)^2\)
\(=\left(2x-5y\right)^2\)
Quan sát 2 vế cửa đẳng thức, xem đẳng thức thuộc hằng đẳng thức nào đã học.
- Từ vị trí số hạng đã biết trong hằng đẳng thức, xác định số hạng cần điền vào dấu *
1) 8x3 + * + * + 27y3 = (* + *)3
2) 8x3 + 12x2y + * + * = (* + *)3
3) x3 - * + * - * = (* - 2y)3
4) (* – 2)(3x + *) = 9x2 – 4
5) 27x3 – 1 = (3x – *)(* + 3x + 1)
6) * + 1 = (3x + 1)(9x2 - * + 1)
7) (2x + 1)2 = * + 4x + *
8) (* - 1)2 = 4x2 - * + 1
9) 9 - * = (3 – 4x)(3 + 4x)
10) (4x2 – 3) = (2x - *)(* + 3 )
a)8x3 + * + * + 27y3 = (* + *)3
=>A=(2x+3y)^3
b) (2x+1)^3
c)(x-2y)^3
d)(3x-2)(3x+2)
e)(3x-1)(9x^2+3x+1)
f)....................
6: \(27x^3+1=\left(3x+1\right)\left(9x^2-3x+1\right)\)
7: \(\left(2x+1\right)^2=4x^2+4x+1\)
8: \(\left(2x-1\right)^2=4x^2-4x+1\)
9: \(9-16x^2=\left(3-4x\right)\left(3+4x\right)\)
Phân tích đa thức 10x - 25 - x2 thành nhân tử bằng phương pháp dùng hằng đẳng thức.
\(10x-25-x^2=-\left(x^2-10x+25\right)\)
\(=-\left(x^2-2.x.5+5^2\right)=-\left(x-5\right)^2\)
10x - 25 - x2
= x2- 10x - 25
= - ( x2 +10x +25)
= -(x2 + 2.x.5+52 )
= - (x+5 )2
\(10x-25-x^2=-\left(x^2-10x+25\right)=-\left(x-5\right)^2\)
Câu 1: Phân tích đa thức 8 - x3 thành nhân tử được?
Câu 2: Cho đẳng thức x2 - 5x + 4 = (x-1).B
Trong đó B là 1 hằng đẳng thức.
Khi đó hệ số tự do của đa thức B là?
Câu 1:8-x^3=2^3-x^3=(2-x)(4+2x+x^2)
Câu 2:Ta có:x^2-5x+4
=(x^2-2x5/2+25/4)-9/4
=(x-5/2)^2-(3/2)^2
=(x-5/2-3/2)(x-5/2+3/2)
=(x-4)(x-1)
->đa thức B là:(x-4)
->hệ số tự do của đa thức B là:-4