Cho tam giác ABC có Aˆ=90o,Bˆ=60o. Kẻ AH vuông góc với BC (H ∈ BC)
So sánh HACˆ và ABCˆ
NT
Những câu hỏi liên quan
Cho tam giác ABC có Aˆ=60o,Bˆ=105o. So sánh độ dài ba cạnh của △ABC
cho tam giác abc có góc b =60o; ab=7cm; bc=15cm;vẽ ah vuông góc với bc(h thuộc bc). Lấy điểm m trên hc sao hm=hb
a)so sánh góc bac và góc acb
b)cm tam giác abm là tam giác đều
tam giác abc có phải là tam giác vuông không? vì sao
a) Xét ΔABC có
BA<BC(gt)
mà góc đối diện với cạnh BA là \(\widehat{ACB}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{BAC}>\widehat{ACB}\)(Quan hệ giữa cạnh và góc đối diện trong tam giác)
b) Xét ΔABH vuông tại H và ΔAMH vuông tại H có
HB=HM(gt)
AH chung
Do đó: ΔABH=ΔAMH(hai cạnh góc vuông)
Suy ra: BA=MA(hai cạnh tương ứng)
Xét ΔBAM có BA=MA(cmt)
nên ΔBAM cân tại A(Định nghĩa tam giác cân)
Xét ΔBAM cân tại A có \(\widehat{B}=60^0\)(gt)
nên ΔBAM đều(Dấu hiệu nhận biết tam giác đều)
Đúng 1
Bình luận (0)
Cho tam giác ABC có ∠A=90o, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác của ∠C và ∠BAH cắt nhau ở I. Chứng minh rằng: ∠(AIC)=90o
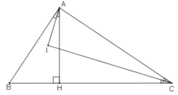
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.
Đúng 1
Bình luận (1)
cho tam giác ABC vuông tại A có góc C = 3 độ ; tia phân giác của góc A cắt BC tại D . Kẻ AH vuông góc với BC ( H thuộc BC )
a, tính góc ADH
b, so sánh góc HAD và góc HAB
c, so sánh góc ABC và góc HAC
a: Xét ΔADC có
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{ADH}=180^0-30^0-45^0\)
hay \(\widehat{ADH}=105^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có góc B=50° a,so sánh AB và AC b,kẻ Ah vuông góc với BC tại h so sánh Bh và AB khi BC=2AB
Cho ABC có Bˆ Cˆ .Gọi AH là đường vuông góc kẻ từ A đến BC
( H thuộc BC) và M là một điểm thuộc đoạn AH.
a)So sánh độ dài BH và CH
b) So sánh độ dài MB và MC
a) Xét ΔABC có Bˆ>CˆB^>C^
mà cạnh đối diện với góc B là AC
và cạnh đối diện với góc C là AB
nên AC>AB
hay AB<AC(Định lí 2 về quan hệ giữa cạnh và góc trong tam giác)
b) Xét ΔABC có AB<AC(cmt)
mà hình chiếu của AB trên BC là HB
và hình chiếu của AC trên BC là HC
nên HB<HC(định lí 2 về quan hệ giữa đường vuông góc, đường xiên và hình chiếu)
c) Xét ΔDBC có HB<HC(cmt)
mà hình chiếu của DB trên BC là HB
và hình chiếu của DC trên BC là HC
nên DB<DC(định lí 1 về quan hệ giữa đường vuông góc, đường xiên và hình chiếu)
Xét ΔDBC có DB<DC(cmt)
mà góc đối diện với DB là góc DCB
và góc đối diện với DC là góc DBC
nên DBCˆ>DCBˆDBC^>DCB^(định lí 1 về quan hệ giữa góc và cạnh trong tam giác)
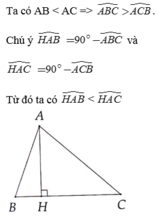
Cho tam giác ABC có ba góc nhọn, AB AC. Kẻ AH vuông góc với BC tại H. So sánh
H
A
B
^
và
H
A
C
^
.
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ AH vuông góc với BC tại H. So sánh và .

CÂU TRẢ LỜI CHÍNH XÁC NÈ
Câu 1: Cho △ABC có góc B 50 độ.a, So sánh các cạnh của △ABCb, Kẻ AH vuông góc với BC tại H. So sánh độ dài cạnh HB và HC Câu 2: Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Kẻ BH và CK vuông góc với đường thẳng AD tại H và Ka, So sánh BH + CK và AB + ACb, So sánh BH + CK và BCNếu△ABC vuông tại B và D là trung điểm BC thì so sánh AH + Ak với 2. AB
Đọc tiếp
Câu 1: Cho △ABC có góc B = 50 độ.
a, So sánh các cạnh của △ABC
b, Kẻ AH vuông góc với BC tại H. So sánh độ dài cạnh HB và HC
Câu 2: Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Kẻ BH và CK vuông góc với đường thẳng AD tại H và K
a, So sánh BH + CK và AB + AC
b, So sánh BH + CK và BC
Nếu△ABC vuông tại B và D là trung điểm BC thì so sánh AH + Ak với 2. AB
a: BH<AB
CK<AC
=>BH+CK<AB+AC
b: BH<BD
CK<CD
=>BH+CD<BD+CD=BC
Đúng 0
Bình luận (0)
Cho tam giác abc có ab < ac kẻ ah vuông góc với bc tại h so sánh độ dài họ và hc
Xét ΔABC có AB<AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB<HC
Đúng 0
Bình luận (0)