Cho hình vuông ABCD tâm O. Tính độ dài |2AB+3OC| (vector hay còn gọi là véc tơ ạ).
CT
Những câu hỏi liên quan
Cho hình chữ nhật ABCD tâm O có cạnh AB=2a,OA=a√5.Tính độ dài véc tơ BC
ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>O là trung điểm chung của AC và BD
ABCD là hình chữ nhật
=>AB=CD=2a; BC=AD
O là trung điểm của AC
=>\(AC=2\cdot AO=2a\cdot\sqrt{5}\)
=>\(BD=2a\sqrt{5}\)
ABCD là hình chữ nhật
=>ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC^2=AC^2-AB^2=\left(2a\sqrt{5}\right)^2-\left(2a\right)^2=20a^2-4a^2=16a^2\)
=>BC=4a
=>\(\left|\overrightarrow{BC}\right|=4a\)
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD tâm O. Gọi I là trung điểm của CD và G là trọng tâm của tam giác ABD. Phân tích véc tơ IG theo 2 véc tơ AB ; AD
1)cho lục giác đều ABCDEF có tâm o.tìm các véc tơ bằng véc tơ EF?
2)cho hình vuông ABDC cạnh bằng a có điểm o. véc tơ AB+AC+AD=2AC và tính |BC+_BA|?
3)cho véc tơ a=(1;2) véc tơ b= (4;3) véc tơ c=(-5)
1) Các vecto bằng vecto EF là:
\(\overrightarrow{EF}=\overrightarrow{DO}=\overrightarrow{OA}=\overrightarrow{CB}\)
Đúng 0
Bình luận (0)
Cho hình thoi ABCD cạnh a có BAD=60 độ. Gọi O là giao điểm của hai đường chéo AC và BD. Gọi O là giao điểm hai đường chéo AC và BD. Gọi G là trọng tâm tam giác ABD, E là điểm đối xứng của O qua D, H là giao điểm AD và GE. Tính độ dài vector AH
Cho hình vuông ABCD có độ dài cạnh là 10 cm . Gọi O là tâm đường tròn nội tiếp hình vuông. Gọi M, N lần lượt là trung điểm của AB; BC. Tính độ dài của cung
M
N
⏜
? A. 2
π
(cm) B. 5
π
(cm) C. 2,5
π
(cm) D. 7,5
π
(cm)
Đọc tiếp
Cho hình vuông ABCD có độ dài cạnh là 10 cm . Gọi O là tâm đường tròn nội tiếp hình vuông. Gọi M, N lần lượt là trung điểm của AB; BC. Tính độ dài của cung M N ⏜ ?
A. 2 π (cm)
B. 5 π (cm)
C. 2,5 π (cm)
D. 7,5 π (cm)
Chọn đáp án C
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
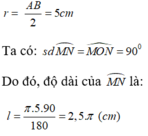
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có cạnh bằng 2a , ABC=60 độ . Tính độ dài của véc tơ AC .
- Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm BC và CD. H là giao điểm AM và BN . Biết HM = 2. Tính véc tơ AB
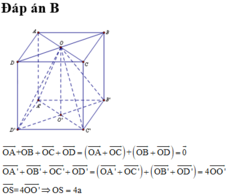
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S sao cho Tính độ dài đoạn OS theo a.
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S sao cho ![]() Tính độ dài đoạn OS theo a.
Tính độ dài đoạn OS theo a.
![]()
![]()
![]()
![]()
Cho tam giác ABC có trực tâm là H, và O là tâm đường tròn ngoại tiếp tam giác ABC Gọi B' là điểm đối xứng với B qua O . CMR véc tơ AH= véc tơ B'C
Xét B thuộc đường tròn (O), B' đối xứng với B qua O => BB' là đường kính của (O)
=> AB' vuông góc AB. Mà CH vuông góc AB nên AB' // CH. Tương tự AH // B'C
Suy ra tứ giác AHCB' là hình bình hành => AH // B'C và AH = B'C => \(\overrightarrow{AH}=\overrightarrow{B'C}\)(đpcm).
Đúng 0
Bình luận (0)