Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M; tia phân giác của góc C cắt AB ở N
a, Chứng minh tứ giác AMCN là hình bình hành
b, Chứng minh 3 đường thẳng AC, MN, BD đồng quy
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.
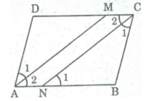
Ta có: ∠ A = ∠ C (tính chất hình bình hành)
∠ A 2 = 1/2 ∠ A ( Vì AM là tia phân giác của ∠ (BAD) )
∠ C 2 = 1/2 ∠ C ( Vì CN là tia phân giác của ∠ (BCD) )
Suy ra: ∠ A 2 = ∠ C 2
Do ABCD là hình bình hành nên AB // CD (gt)
Hay AN // CM (1)
Mà ∠ N 1 = ∠ C 2 (so le trong)
Suy ra: ∠ A 2 = ∠ N 1
⇒ AM // CN (vì có cặp góc ở vị trí đồng vị bằng nhau) (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
Cho Hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc c cắt AB ở N. Chứng minh rằng AMCN là hình bình hành
ABCD là hình bình hành
DAB=BCD,B=D
mà DAM=MAB=DAB/2(AM tia pg)
BCN=NCD=BCD/2(NC tia pg)
=>NAM=NCM,NCB=DAM
lại có ANC=B+NCB(góc ngoài tgBCN)
AMC=D+DAM(góc ngoài tgBCN)
=>ANC=AMC
xét tứ giác AMCN
NAM=NCM,ANC=AMC
=>AMCN là hình bình hành
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N.
Chứng minh rằng AMCN là hình bình hành ?
Vì ABCD là hình bình hành
⇒ AB//CD
Ta có :
AM là p/g của A
NC là p/g của C
⇒ DAM=BCN
⇒ AM//NC ( slt )
Xét hình thang AMCN có
AD//BC ( gt)
AM//CD (cmt)
⇒ AMCN là hình bình hành
1.Cho hình bình hành ABCD có AB=2BC. Gọi M là trung điểm của CD. Cmr:
a)AM,BM lần lượt là phân giác của góc A,góc B của hình bình hành ABCD
b)Tính góc AMB?
2. Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác góc C cắt AB ở N
a)Tứ giác AMCN là hình gì?Vì sao?
b) Cmr : BM=DN
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng
a) AMCN là hình bình hành.
b) 3 đường AC, MN, BD đồng quy
a: Xét ΔDAM và ΔBCN có
\(\widehat{D}=\widehat{B}\)
DA=BC
\(\widehat{DAM}=\widehat{BCN}\)
Do đó: ΔDAM=ΔBCN
Suy ra: AM=CN và DM=BN
Ta có: AN+NB=AB
CM+MD=CD
mà AB=CD
và DM=BN
nên AN=CM
Xét tứ giác AMCN có
AN//CM
AM//CN
Do đó: AMCN là hình bình hành
Bài 1 :Cho hình bình hành ABCD .Tia phân giác của góc A cắt CD ở M . Tia phân giác của góc C cắt AB ở N. CMR AMCN là hình bình hành
Bài 2: Cho hình bình hành ABCD .Gọi I, K là trung điểm của CD ,AB. Đường chéo BD cắt AI ,CK ở E ,F .CMR DE=EF=FB
Mọi người ơi giúp mk với mk cần gấp !!!
Bài 1 :Cho hình bình hành ABCD .Tia phân giác của góc A cắt CD ở M . Tia phân giác của góc C cắt AB ở N. CMR AMCN là hình bình hành
Bài 2: Cho hình bình hành ABCD .Gọi I, K là trung điểm của CD ,AB. Đường chéo BD cắt AI ,CK ở E ,F .CMR DE=EF=FB
Mọi người ơi giúp mk với mk cần gấp !!!
a) * Vì ABCD là hình bình hành(gt)
=> \(\widehat{A}=\widehat{C}\); \(\widehat{B}=\widehat{D};AD=BC;AB//CD\)( tính chất)
_ Ta có AM là tia phân giác của GÓC A => \(\widehat{A_1}=\widehat{A_2}=\frac{\widehat{A}}{2}\left(1\right)\)
_Ta có CN là tia phân giác của GÓC C =>\(\widehat{C_1}=\widehat{C_2}=\frac{\widehat{C}}{2}\left(2\right)\)
_ Từ (1) (2) => \(\widehat{A_1}=\widehat{C_2}\)
* Xét \(\Delta ADM\) và \(\Delta CBN\)có:
\(\widehat{A_1}=\widehat{C_2}\)( cmt)
AD=BC( cmt)
GÓC B=GÓC D
=> \(\Delta ADM=\Delta CBN\left(g.c.g\right)\)
=>AM=CN (3) ( 2 cạnh tuiwng ứng)
\(\widehat{M_1}=\widehat{N_1}\) ( 2 góc tương ứng)
* Mà AB//CD( gt)
\(N\in AB;M\in CD\left(gt\right)\)
=>BN//CM => \(\widehat{N_1}=\widehat{C_1}\)( 2 góc SLT)
=> \(\widehat{M_1}=\widehat{C_1}\)
Mà 2 góc này ở vị trí Đồng vị
=> AM//CN(4)
* Từ (3)(4)
=> AMCN là hình bình hành
_ Cậu tự vẽ hình xong đặt chỉ số ạ_
_tham khảo bài àm trên đây ạ, chúc cậu học tốt '.'
Bài 1 : Cho hình bình hành ABCD ( AB > BC ) . Tia phân giác của góc D cắt AB ở E , tia phân giác của góc B cắt CD ở F . a ) Chứng minh DE // BF b ) Tứ giác DEBF là hình gì Bài 2 : Cho hình bình hành ABCD . gọi K , I lần lượt là trung điểm của các cạnh AB , CD . Gọi M , N lần lượt là giao điểm của AI , CK với đường chéo BD . Chứng minh AC , BD , IK đồng quy tại một điểm
Bài 2:
AK=AB/2
CI=CD/2
mà AB=CD
nên AK=CI
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường(1)
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,KI,BD đồng quy
Bài 1:
a: \(\widehat{ADE}=\widehat{EDF}=\dfrac{1}{2}\cdot\widehat{ADC}\)
\(\widehat{ABF}=\widehat{CBF}=\dfrac{1}{2}\cdot\widehat{ABC}\)
mà \(\widehat{ADC}=\widehat{ABC}\)
nên \(\widehat{ADE}=\widehat{EDF}=\widehat{ABF}=\widehat{CBF}\)
Xét ΔEAD và ΔFCB có
\(\widehat{A}=\widehat{C}\)
AD=CB
\(\widehat{EDA}=\widehat{FBC}\)
Do đó: ΔEAD=ΔFCB
=>\(\widehat{AED}=\widehat{CFB}\)
=>\(\widehat{EDF}=\widehat{CFB}\)
mà hai góc này đồng vị
nên DE//BF
b: Xét tứ giác DEBF có
DE//BF
BE//DF
Do đó: DEBF là hình bình hành
cho hình bình hành ABCD. các tia phân giác của góc A, góc C cắt CD và AB lần lượt ở M, N. CM: a)tứ giác AMCN là hình bình hành b)BM=DN
Bạn tự vẽ hình nha
a) Do ABCD là hình bình hành ⇒ Góc A = góc C
⇒ \(\dfrac{1}{2}\)góc A = \(\dfrac{1}{2}\)góc C ⇒ Góc DAM = Góc BCN
Xét tam giác ADM và tam giác CBN có:
AD = BC ( ABCD là hình bình hành)
Góc DAM = góc CBN ( Chứng minh trên )
Góc ADB = góc ABC ( ABCD là hình bình hành )
⇒ Tam giác ADM = tam giác CBN (g.c.g)
⇒ BN = DM ( 2 cạnh tương ứng )
Vì ABCD là hình bình hành ⇒ AB = CD
⇒ BN + AN = CM + DM.
Mà BN = DM ⇒ AN = MC. Do AN song song với MC ( vì AB song song với CD)
ANCM là hình bình hành.
b) Xét tứ giác BMDN có BN = DM ; BN song song với DM ( do AB song song với CD)
⇒ BMDN là hình bình hành ⇒ BM = DN
Cho hình bình hành ABCD ( AB> BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a. c/m DE // BF
b. tứ giác DEBF là hình j