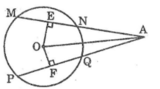
Cho hình vẽ sau, trong đó MN=PQ. Chứng minh rằng:
a, AE=AF
b, AN=AQ.
NQ
Những câu hỏi liên quan
Cho hình bên, trong đó MN = PQ. Chứng minh rằng: AN = AQ
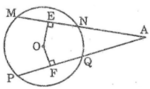
Ta có: OE ⊥ MN (gt)
Suy ra EN = (1/2).MN (đường kính vuông góc với dây cung) (1)
OF ⊥ PQ (gt)
Suy ra FQ = (1/2).PQ (đường kính vuông góc với dây cung) (2)
Mặt khác: MN = PQ (gt) (3)
Từ (1), (2) và (3) suy ra: EN = FQ (4)
Mà AE = QF (chứng minh trên) (5)
Từ (4) và (5) suy ra: AN + NE = AQ + QF (6)
Từ (5) và (6) suy ra: AN = AQ
Đúng 0
Bình luận (0)
Cho hình 74 trong đó MN = PQ.
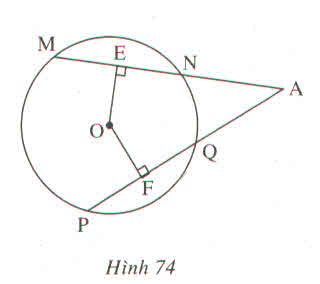
Chứng minh rằng:
a) AE = AF
b) AN = AQ
Cho hình vẽ bên. Chứng minh rằng:
a) MNQ =PQN;
b) MN song song với PQ ;
c) MQ song song với NP ;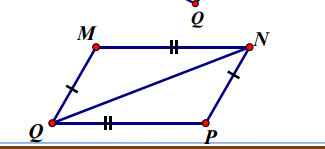 
a) Xét \(\Delta MNQvà\Delta PQN\) ta có:
\(\left\{{}\begin{matrix}MN=PQ\\MQ=NP\\NQ:cạnhchung\end{matrix}\right.\)
\(\Rightarrow\Delta MNQ=\Delta PQN\)
Đúng 1
Bình luận (0)
Cho hình bên, trong đó MN = PQ. Chứng minh rằng: AE = AF
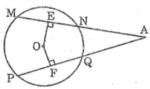
Nối OA
Ta có: MN = PQ (gt)
Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OAE và OAF, ta có:
OA chung
OE = OF (chứng minh trên)
Suy ra: ΔOAE = ΔOAF (cạnh huyền, cạnh góc vuông)
Suy ra: AE = AF
Đúng 0
Bình luận (0)
Cho hình thang ABCD có đáy lớn CD. Qua A vẽ đường thẳng song song với BC cắt DC tại K. Qua B vẽ đường thẳng song song với AD cắt DC tại I..BI cắt AC tại F, AK cắt BD tại E. Chứng minh rằng:
a)Tam giác AFB đồng dạng với tam giác CFI
b) AE. KD = AB. EK
c) AB2 = CD. EF
Giúp e ý c với
Cho hình bình hành MNPQ (MN>PQ) tia phân giác của góc Q cắt MN tại A, tia phân giác góc N cắt PQ tại B. Chứng minh ANBQ là hình bình hành và AQ=BN Giúp mình với mn
Cho tứ giác MNPQ, F, H, K lần lược là trung điểm của MN, NP,PQ, MQ. Chứng minh rằng:
a) Tứ giác EFHK là hình thoi
b) EG vương góc với HF
Cho 2 tia Ax và Ay , Trên tia đối của à vẽ tia At , trên tia đối của tia Ay vẽ tia Az.
A. Trên đường thẳng tx lấy hai điểm M, N sao cho A nằm giữa M,N biết AN = 2cm , AM = 7cm
B. Trên đường thẳng zy lấy 2 điểm PQ sao cho nằm cùng phía với Ay, AP= 1/4 AQ biết AB = 2 cm
C. Vẽ hình , tính AQ = ? AN , MN = ? , PQ = ?
Giải giùm với !!!
Bài 7: Cho hình vẽ bên Biết MN//PQ, MN = PQ. Chứng minh MQ = NP và MQ //NP.
MN//PQ, MN = PQ⇒MNPQ là hình bình hành⇒MQ=NP, MQ //NP.
Đúng 1
Bình luận (0)
Xét tứ giác MNPQ có
MN//PQ
MN=PQ
Do đó: MNPQ là hình bình hành
=>MQ//NP và MQ=NP
Đúng 0
Bình luận (0)
MN//PQ, MN = PQ⇒MNPQ là hình bình hành⇒MQ=NP, MQ //N
Đúng 0
Bình luận (0)