giải bài toán bằng cách lập phương trình : x^5+x+1
TM
Những câu hỏi liên quan
Bài 1 : Một Hcn có chu vi 600m. Nếu chiều dài giảm đi 1/5 của nó, chiều rộng tăng thêm 3/10 của nó thì chu vi Hcn không đổi. Tính chiều dài và chiều rộng của Hcn.
Giải bằng 2 cách :
Cách 1 : Giải bài toán bằng cách lập phương trình
Cách 2 ; Giải bài toán bằng cách lập hệ phương trình
Bài 1 : Một Hcn có chu vi 600m. Nếu chiều dài giảm đi 1/5 của nó, chiều rộng tăng thêm 3/10 của nó thì chu vi Hcn không đổi. Tính chiều dài và chiều rộng của Hcn.
Giải bằng 2 cách :
Cách 1 : Giải bài toán bằng cách lập phương trình
Cách 2 ; Giải bài toán bằng cách lập hệ phương trình
Cho hệ phương trình\(\hept{\begin{cases}x+y=40\\\left(x+3\right)\left(y+5\right)=xy+195\end{cases}}\)
Anh (chị) hãy thiết kế một bài toán thực tế mà khi giải bài toán bằng cách lập hệ
phương trình ta có hệ phương trình trên. Hãy giải bài toán đã thiết kế.
Ai thiết kế bài toán hộ cái. Bí chẳng có ý tưởng
Đề : Một hình chữ nhật có chu vi bằng 80 cm. Tăng chiều rộng lên 3cm; tăng chiều dài lên 5 cm thì diện tích tăng thêm 195 cm^2.
Tìm chiều dài và chiều rộng ban đầu.
II. TỰ LUẬN: (6 điểm) Bài 1: ( 3 điểm ) Giải phương trình : a) x-14-4 (1-2x) b) x+2 1 x+6 x-2 xx(x-2) Bài 2: ( 3 điểm ) Giải bài toán bằng cách lập phương trình : Một người đi ôtô từ A đến B với vận tốc 50 km/h và quay về liền từ B về với vận tốc là 40 km/h. Cả đi và về mất 5 giờ 24 phút . Tính quãng đường AB?Giải giúp với ạ đang cần gấp:
Đọc tiếp
II. TỰ LUẬN: (6 điểm)
Bài 1: ( 3 điểm ) Giải phương trình :
a) x-14-4 (1-2x)
b)
x+2 1 x+6
x-2 xx(x-2)
Bài 2: ( 3 điểm ) Giải bài toán bằng cách lập phương trình :
Một người đi ôtô từ A đến B với vận tốc 50 km/h và quay về liền từ B về với vận tốc là 40
km/h. Cả đi và về mất 5 giờ 24 phút . Tính quãng đường AB?
Giải giúp với ạ đang cần gấp:<
2:
Gọi độ dài AB là x
Thời gian đi là x/50
Thời gian về là x/40
Theo đề, ta có: x/50+x/40=5,4
=>x=120
Đúng 0
Bình luận (0)
Câu 1: Rút gọn biểu thức sau: A left(sqrt{3}+1right)sqrt{dfrac{14-6sqrt{3}}{5+sqrt{3}}}Câu 2: 2.1 Giải các phương trình sau a/ x2 (x-1)(3x-2)b/ 9x4+5x2-4 02.2 Giải bài toán sau bằng cách lập phương trình: một đội xe cần chở 120 tấn hàng, hôm làm việc có 2 xe bị điều đi nơi khác nên mỗi xe phải,chở thêm 3 tấn nữa. Tính số xe lúc đầu của độiBài 3: Cho parabol (P): y ax2 và đường thẳng (d): y mx+ 1a) Tìm a biết (P) đi qua điểm A (2;-4). Vẽ (P) với a tìm được b) Tìm giá trị của m để đường thẳng (d...
Đọc tiếp
Câu 1: Rút gọn biểu thức sau: A = \(\left(\sqrt{3}+1\right)\sqrt{\dfrac{14-6\sqrt{3}}{5+\sqrt{3}}}\)
Câu 2:
2.1 Giải các phương trình sau
a/ x2 = (x-1)(3x-2)
b/ 9x4+5x2-4= 0
2.2 Giải bài toán sau bằng cách lập phương trình: một đội xe cần chở 120 tấn hàng, hôm làm việc có 2 xe bị điều đi nơi khác nên mỗi xe phải,chở thêm 3 tấn nữa. Tính số xe lúc đầu của đội
Bài 3: Cho parabol (P): y= ax2 và đường thẳng (d): y= mx+ 1
a) Tìm a biết (P) đi qua điểm A (2;-4). Vẽ (P) với a tìm được
b) Tìm giá trị của m để đường thẳng (d) tiếp xúc với parabol (P). Tìm tọa độ tiếp điểm
Bài 4: Cho phương trình: x2 -(2m -1)x + m2 -1 = 0, m là tham số
a) Tìm các giá trị của m để phương trình có 2 nghiệm phân biệt
b) Gọi X1x2 lần lượt là hai nghiệm của phương trình. Tìm m để phương trình có hai nghiệm thỏa mản: (x1 -x2)2 = x1 -3x2
Bài 5: Cho đường tròn (O;R) và một điểm nằm ngoài đường tròn. Từ A kẻ 2 tiếp tuyến AB,AC và một cát tuyến AMN đến O
a. Chứng minh: AB2 = AM.AN
b/ Gọi i là trung điểm MN,Ci cắt đường tròn tại K. Chứng minh A, B, i, O
cùng thuộc một đường tròn và BK//MN
c) gọi H là giao điểm của AO và BC. Chứng minh tứ giác HMNO nội tiếp và HB là phân giác của góc MHN
1.\(A=\left(\sqrt{3}+1\right)\sqrt{\dfrac{14-6\sqrt{3}}{5+\sqrt{3}}}=\left(\sqrt{3}+1\right)\sqrt{\dfrac{\left(14-6\sqrt{3}\right)\left(5-\sqrt{3}\right)}{\left(5+\sqrt{3}\right)\left(5-\sqrt{3}\right)}}\)
\(=\left(\sqrt{3}+1\right)\sqrt{\dfrac{44\left(2-\sqrt{3}\right)}{22}}=\left(\sqrt{3}+1\right)\sqrt{4-2\sqrt{3}}=\left(\sqrt{3}+1\right)\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)=2\)
Đúng 1
Bình luận (0)
2.1.a) \(x^2=\left(x-1\right)\left(3x-2\right)\Leftrightarrow x^2=3x^2-5x+2\Leftrightarrow2x^2-5x+2=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{2}\end{matrix}\right.\)
b) \(9x^4+5x^2-4=0\Leftrightarrow9x^4+9x^2-4x^2-4=0\)
\(\Leftrightarrow9x^2\left(x^2+1\right)-4\left(x^2+1\right)=0\Leftrightarrow\left(x^2+1\right)\left(9x^2-4\right)=0\)
mà \(x^2+1>0\Rightarrow9x^2=4\Rightarrow x^2=\dfrac{4}{9}\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
2) Gọi số xe lúc đầu của đội là a(xe) \(\left(a\in N,a>0\right)\)
Theo đề,ta có: \(\left(a-2\right)\left(\dfrac{120}{a}+3\right)=120\Leftrightarrow120+3a-\dfrac{240}{a}-6=120\)
\(\Leftrightarrow\dfrac{3a^2-6a-240}{a}=0\Rightarrow3a^2-6a-240=0\Rightarrow a^2-2a-80=0\)
\(\Leftrightarrow\left(a+8\right)\left(a-10\right)=0\) mà \(a>0\Rightarrow a=10\)
Đúng 1
Bình luận (0)
Bài 1 Bài 2
Bài 2
2.1
 Bài 4
Bài 4
 Bạn tham khảo nha. Chúc bạn học tốt
Bạn tham khảo nha. Chúc bạn học tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải bài toán bằng cách lập phương trình
Đọc tiếp
Giải bài toán bằng cách lập phương trình
a: =>3x=-7/2-1=-9/2
=>x=-3/2
b: =>2(x+4)+3x+2=70
=>2x+8+3x+2=70
=>5x+10=70
hay x=12
c: \(\Leftrightarrow\left(3x-5\right)\left(3x-5-6x-10\right)=0\)
=>(3x-5)(-3x-15)=0
=>x=5/3 hoặc x=-5
d: \(\Leftrightarrow\left(x+1\right)\left(x+2\right)-5\left(x-2\right)=-12+x^2-4\)
\(\Leftrightarrow x^2+3x+2-5x+10=x^2-16\)
=>-2x+12=-16
=>-2x=-28
hay x=14(nhận)
Đúng 4
Bình luận (0)
Giải bài toán bằng cách lập phương trình
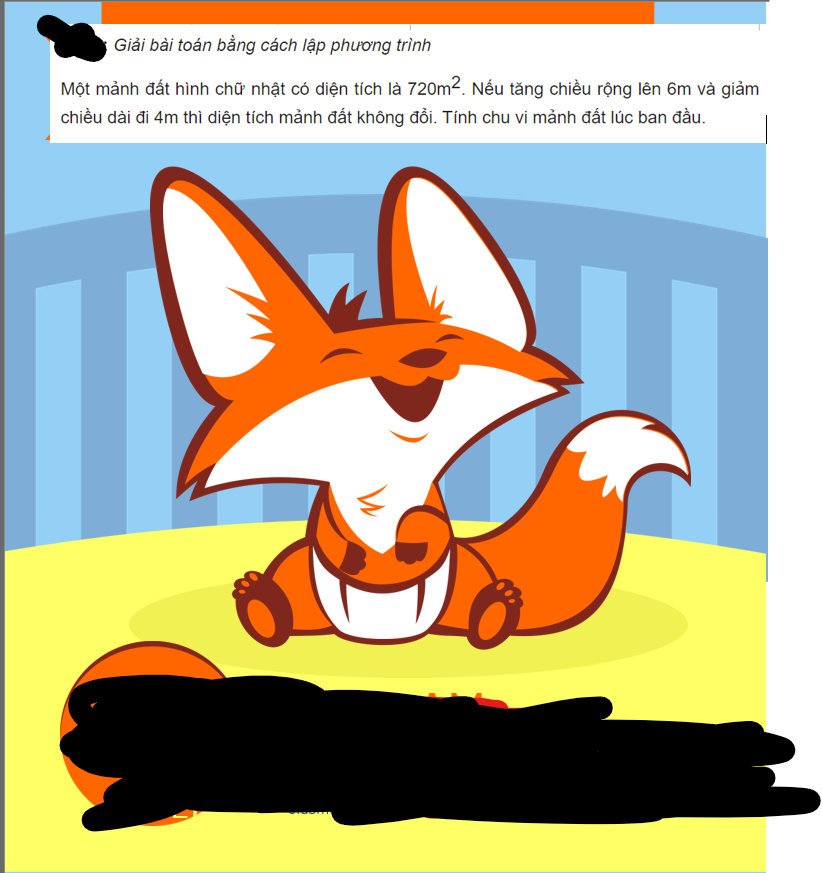
Gọi chiều rộng của mảnh đất hình chữ nhật là \(x\left(m,x>0\right)\)
Chiều dài của mảnh đất hình chữ nhật: \(\dfrac{720}{x}\left(m\right)\)
Chiều rộng mới của mảnh đất hình chữu nhật \(x+6\left(m\right)\)
Chiều dài mới của mảnh đất hình chữ nhật \(\dfrac{720}{x}-4\left(m\right)\)
Theo đề bài, ta có PT: \(\left(x+6\right)\left(\dfrac{720}{x}-4\right)=720\)
\(\Leftrightarrow720-4x+\dfrac{4320}{x}-24=720\)
\(\Leftrightarrow720x-4x^2+4320-24x-720x=0\)
\(\Leftrightarrow-4x^2-24x+4320=0\)
\(\Leftrightarrow\left(x-30\right)\left(x+36\right)=0\)
Vậy \(x=30\) (thoả mãn)
Chiều rộng của mảnh vườn hình chữ nhật 24m, chiều dài của mảnh vườn hình chữ nhật 30m
Chu vi của mảnh đất hình chữ nhật: \(\left(24+30\right).2=108m\)
Đúng 3
Bình luận (1)
giải bài toán bằng cách lập phương trình
cách giải các bài toán bằng cách lập phương trình hoặc hệ phương trình thường gặp ?







