A = 4 / 1 x 3 x5 + 4 / 3 x 5 x7
H24
Những câu hỏi liên quan
Giải các phương trình sau:1) 2 1 5 x 2) 2 1 5 x x 3) 3 1 2 x x 4) 3 2 2 x x5) 2 1 5 x x 6) 3 2 x x7) 2 3 2 1 x x 8) 2 1 4 1 0 x x 29) 2 5 4 3 1 1 23 2 3 1x xx x x x 10) 1 7 3 23 3 9x x xx x x 11) 5 296 2 1 3 116 4 4x xx x x 12) 2 412 1 2 1 2 1 2 1x xx x x x 13) 2 1 2 22 2xx x x x 14) 22 42 6 2 2 2 3
Đọc tiếp
Giải các phương trình sau:
1) 2 1 5 x 2) 2 1 5 x x
3) 3 1 2 x x 4) 3 2 2 x x
5) 2 1 5 x x 6) 3 2 x x
7) 2 3 2 1 x x 8) 2 1 4 1 0 x x 2
9) 2 5 4 3 1 1 2
3 2 3 1
x x
x x x x
10) 1 7 3 2
3 3 9
x x x
x x x
11) 5 296 2 1 3 1
16 4 4
x x
x x x
12)
2 4
1
2 1 2 1 2 1 2 1
x x
x x x x
13) 2 1 2 2
2 2
x
x x x x
14) 22 4
2 6 2 2 2 3
MN KB MIK NHA !!!!!!!!!!!!!!!!!!!!!
1 X 2 x 3 x 4 x5 x 6 x7+10-12x12 = ?
mn kb mik nha !
Xem thêm câu trả lời
546 + 54 =
1 x 2 x3 x 4 x5 x6 x7 x8 x9 =
546 + 54 = 600
1 x 2 x3 x 4 x5 x6 x7 x8 x9 = 362880
Đúng 0
Bình luận (0)
546 + 54 = 600
1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9
= 362880
~ Học tốt ~
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 4 : phân tích đa thức thành nhân tử rồi tính giá trị của các biểu thức sau :
a, A= 4(x - 2) (x+1) + (2x - 4)2 +(x+1)2 tại x = \(\dfrac{1}{2}\)
b, B= x9 - x7 - x6 - x5 + x4 + x3 + x2 - 1 tại x=1
a,
\(A=4(x-2)(x+1)+(2x-4)^2+(x+1)^2\\=[2(x-2)]^2+2\cdot2(x-2)(x+1)+(x+1)^2\\=[2(x-2)+(x+1)]^2\\=(2x-4+x+1)^2\\=(3x-3)^2\)
Thay $x=\dfrac12$ vào $A$, ta được:
\(A=\Bigg(3\cdot\dfrac12-3\Bigg)^2=\Bigg(\dfrac{-3}{2}\Bigg)^2=\dfrac94\)
Vậy $A=\dfrac94$ khi $x=\dfrac12$.
b,
\(B=x^9-x^7-x^6-x^5+x^4+x^3+x^2-1\\=(x^9-1)-(x^7-x^4)-(x^6-x^3)-(x^5-x^2)\\=[(x^3)^3-1]-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1)-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1-x^4-x^3-x^2)\\=(x^3-1)(x^6-x^4-x^2+1)\)
Thay $x=1$ vào $B$, ta được:
\(B=(1^3-1)(1^6-1^4-1^2+1)=0\)
Vậy $B=0$ khi $x=1$.
$Toru$
Đúng 1
Bình luận (0)
Cho f(x) 1+x3+x5+x7+...+x51f(x) 1+x3+x5+x7+...+x51. Khi đó f(-1) bằng: A.– 24 B.26 C.– 25 D.– 23
Đọc tiếp
Cho . Khi đó f(-1) bằng:
A.– 24
B.26
C.– 25
D.– 23
Tính tổng
A=1 x 5 x 51 x52 x 53x54x55x56x57x58x59x510
kết quả là 5 ^ 56
bạn ơi bằng
5mũ 56
học tốt nha
tính bằng 2 cách
a) 4 x 6 x 8 b) 3x 9 x7
2 x 6 x5 4 x 7 x 3
a) 4 x 6 x 8 = 24 x 8 = 224
4 x 6 x 8 = 4 x 48 = 224
2 x 6 x 5 = 12 x 5 = 60
2 x 6 x 5 = 2 x 5 x 6 = 10 x 6 = 60
b) 3 x 9 x 7 = 27 x 7 = 189
3 x 9 x 7 = 3 x 63 = 189
4 x 7 x 3 = 28 x 3 = 84
4 x 7 x 3 = 4 x 21 = 84
Đúng 0
Bình luận (0)
a) 4/5 x 6/7 b)2/3 x 3/5 c)1/2 x1/3 d) 1/5 x5/7
a) 24/35
b) 2/5
c) 1/6
d) 1/7
Đúng 2
Bình luận (0)
Tính f(x) – g(x) với:
f(x) = x7 – 3x2 – x5 + x4 – x2 + 2x – 7
g(x) = x – 2x2 + x4 – x5 – x7 – 4x2 – 1
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x7 – 3x2 – x5 + x4 – x2 + 2x – 7
= x7 - (3x2+ x2) – x5+ x4 + 2x – 7
= x7 – 4x2 – x5+ x4 + 2x – 7
= x7 – x5 + x4 – 4x2 + 2x - 7
g(x) = x – 2x2 + x4 – x5 – x7 – 4x2 – 1
= x – ( 2x2 + 4x2) + x4 – x5 –x7 – 1
= x – 6x2 + x4 – x5 – x7 – 1
= -x7 – x5 + x4 – 6x2 + x – 1
* f(x) – g(x)
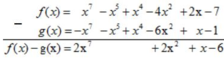
Vậy f(x) – g(x) = 2x7 + 2x2 + x - 6
Đúng 0
Bình luận (0)






