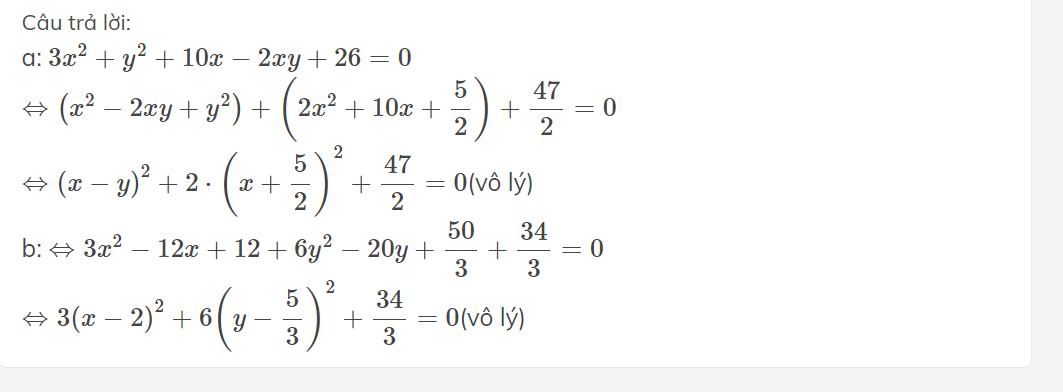Chứng minh rằng ko có giá trị nào thỏa mãn đẳng thức sau 3x^2+6y^2 -12x-20y+40=0
BL
Những câu hỏi liên quan
Chứng minh không có giá trị x,y nào thỏa mãn đẳng thức `3x^2+6y^2-12x-20y+40=0`
\(3x^2+6y^2-12x-20y+40=0\)
\(\Rightarrow\left(3x^2-12x+12\right)+\left(6y^2-12y+6\right)+22=0\)
\(\Rightarrow3\left(x^2-4x+4\right)+6\left(y^2-2y+1\right)+22=0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-1\right)^2+22=0\)
Ta thấy: \(3\left(x-2\right)^2\ge0\forall x\)
\(6\left(y-1\right)^2\ge0\forall y\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-1\right)^2\ge0\forall x;y\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-1\right)^2+22>0\forall x;y\)
Mặt khác: \(3\left(x-2\right)^2+6\left(y-1\right)^2+22=0\)
Suy ra: Không có giá trị nào của x; y thoả mãn yêu cầu đề bài.
#Ayumu
Đúng 2
Bình luận (0)
Chứng minh rằng không có x, y nào thỏa mãn đẳng thức
3x2+y2+10x-2xy+26=0
3x2+6y2-12x-20y+40=0
4x2+3y2-4x+30y+78=0
bạn c/m cho nó lớn hơn hoặc nhỏ hơn 0 đi mk ngại làm vì hơi nhìu ^.^ sory
Đúng 0
Bình luận (0)
bài này chỉ có hsg như tui, alibaba nguyễn, hoàng lê bảo ngọc ..... làm dc
Đúng 0
Bình luận (0)
câu c:(4x²-4x+1) + (3y²+30y+75) + 2
<=> (2x-1)²+ 3(y²+10y+25) +2
<=> (2x-1)²+ 3(y+5)²+2
Ta có: (2x-1)²≥ 0; 3(y+5)²≥ 0; 2>0
=> (2x-1)²+ 3(y+5)²+2 >0
Đúng 0
Bình luận (0)
3) Chứng minh rằng không có các số x; y nào thỏa mãn mỗi đẳng thức sau:
a) 3x^2+y^2+10x-2xy+26=0
b) 4x^2+3y^2-4x+30y+78=0
c) 3x^2+6y^2-12x-20y+40=0
CMR: KHÔNG CÓ SỐ X;Y NÀO THỎA MÃN ĐẲNG THỨC SAU :
A) 4X2+3Y2-4X+30Y+78=0
B) 3X2+6Y2-12X-20Y+40=0
a) 4x2+3y2-4x+30y+78
=4x2-4x+1+3y2+30y+75+2
=(4x2-4x+1)+3(y2+10y+25)+2
=(2x-1)2+3(y+5)2+2>0 với mọi x
=>ko có x;y nào thỏa mãn
b)3x2+6y2-12x-20y+40
\(=3\left(x^2-4x+4\right)+6\left(y^2-\frac{10}{3}+\frac{25}{9}\right)+\frac{34}{3}\)
\(=3\left(x-2\right)^2+6\left(y-\frac{5}{3}\right)^2+\frac{34}{3}>0\) với mọi x
=>ko có x;y nào thỏa mãn
Đúng 1
Bình luận (0)
3) Chứng minh rằng không có các số x; y nào thỏa mãn mỗi đẳng thức sau:
a) 3x2+y2+10x-2xy+26=0
b) 4x2+3y2-4x+30y+78=0
c) 3x2+6y2-12x-20y+40=0
https://olm.vn/hoi-dap/question/164374.html
Đúng 0
Bình luận (0)
Chứng minh rằng không có các số x,y nào thỏa mãn mỗi đẳng thức sau:a) 3x^2+y^2+10x-2xy+260b) 3x^2+6y^2-12x-20y+400c) 4x^2+3y^2-4x+30y+780
Đọc tiếp
Chứng minh rằng không có các số x,y nào thỏa mãn mỗi đẳng thức sau:
a) 3x^2+y^2+10x-2xy+26=0
b) 3x^2+6y^2-12x-20y+40=0
c) 4x^2+3y^2-4x+30y+78=0
a) 3x^2+y^2+10x-2xy+26=0
b) 3x^2+6y^2-12x-20y+40=0
c) 4x^2+3y^2-4x+30y+78=0
a: \(3x^2+y^2+10x-2xy+26=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(2x^2+10x+\dfrac{5}{2}\right)+\dfrac{47}{2}=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\cdot\left(x+\dfrac{5}{2}\right)^2+\dfrac{47}{2}=0\)(vô lý)
b: \(\Leftrightarrow3x^2-12x+12+6y^2-20y+\dfrac{50}{3}+\dfrac{34}{3}=0\)
\(\Leftrightarrow3\left(x-2\right)^2+6\left(y-\dfrac{5}{3}\right)^2+\dfrac{34}{3}=0\)(vô lý)
Đúng 0
Bình luận (0)
a) Chứng minh các biểu thức sau luôn dương với mọi giá trị của biến
1) x3 + 4y2 - 4x - 4y + 2016
2) 4x2 + 4xy + 17y2 - 8y + 1
3) 2x2 - 5x + 13
b) Chứng minh rằng không có các số x,y thỏa mãn mỗi đẳng thức sau
1) 3x2 + y2 +10x - 2xy + 26 0
2) 3x2 + 6y2 - 12x - 20y + 40 0
Huhu các bạn ơi giúp mình với mai mình phải nộp rồi mà chưa nghĩ ra
Đọc tiếp
a) Chứng minh các biểu thức sau luôn dương với mọi giá trị của biến
1) x3 + 4y2 - 4x - 4y + 2016
2) 4x2 + 4xy + 17y2 - 8y + 1
3) 2x2 - 5x + 13
b) Chứng minh rằng không có các số x,y thỏa mãn mỗi đẳng thức sau
1) 3x2 + y2 +10x - 2xy + 26 = 0
2) 3x2 + 6y2 - 12x - 20y + 40 = 0
Huhu các bạn ơi giúp mình với mai mình phải nộp rồi mà chưa nghĩ ra
Bài a:
1) \(x^2+4y^2-4x-4y+2016\)
\(=\left(x^2-4x+4\right)+\left(4y^2-4y+1\right)+2011\)
\(=\left(x-2\right)^2+\left(2y-1\right)^2+2011\)
Vì \(\left(x-2\right)^2\ge0\)
\(\left(2y-1\right)^2\ge0\)
\(2011>0\)
\(\Rightarrow\left(x-2\right)^2+\left(2y-1\right)^2+2011>0\)
Vậy biểu thức trên luôn dương với mọi giá trị của biến
2) \(4x^2+4xy+17y^2-8y+1\)
\(=\left(4x^2+4xy+y^2\right)+\left(16y^2-8y+1\right)\)
\(=\left(2x+y\right)^2+\left(4y-1\right)^2\)
Vì \(\left(2x+y\right)^2\ge0\)
\(\left(4y-1\right)^2\ge0\)
\(\Rightarrow\left(2x+y\right)^2+\left(4y-1\right)^2\ge0\)
Vậy biểu thức trên luôn dương với mọi giá trị của biến
3) \(2x^2-5x+13\)
\(=2\left(x^2-\dfrac{5}{2}x+\dfrac{13}{2}\right)\)
\(=2\left(x^2-2.x.\dfrac{5}{4}+\dfrac{25}{16}-\dfrac{25}{16}+\dfrac{13}{2}\right)\)
\(=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{79}{8}\)
Vì \(2\left(x-\dfrac{5}{4}\right)^2\ge0\)
\(\dfrac{79}{8}>0\)
\(\Rightarrow2\left(x-\dfrac{5}{4}\right)^2+\dfrac{79}{8}>0\)
Vậy biểu thức trên luôn dương với mọi giá trị của biến x
Bài b:
1) \(3x^2+y^2+10x-2xy+26=0\)
\(\Rightarrow\left(x^2-2xy+y^2\right)+\left(2x^2+10x+26\right)=0\)
\(\Rightarrow\left(x-y\right)^2+2\left(x^2+5x+13\right)=0\)
\(\Rightarrow\left(x-y\right)^2+2\left(x^2+2.x.\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{25}{4}+13\right)=0\)
\(\Rightarrow\left(x-y\right)^2+2\left(x+\dfrac{5}{2}\right)^2+\dfrac{27}{2}=0\)
Vì \(\left(x-y\right)^2\ge0\)
\(2\left(x+\dfrac{5}{2}\right)^2\ge0\)
\(\dfrac{27}{2}>0\)
\(\Rightarrow\left(x-y\right)^2+2\left(x+\dfrac{5}{2}\right)^2+\dfrac{27}{2}>0\)
Vậy không có các số x,y thỏa mãn đẳng thức trên
2) \(3x^2+6y^2-12x-20y+40=0\)
\(\Rightarrow\left(3x^2-12x+12\right)+\left(6y^2-20y\right)+40=0\)
\(\Rightarrow3\left(x^2-4x+4\right)+6\left(y^2-\dfrac{3}{10}y\right)+28=0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y^2-2.y.\dfrac{3}{20}+\dfrac{9}{400}-\dfrac{9}{400}\right)+28=0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-\dfrac{3}{20}\right)^2-\dfrac{27}{200}+28=0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-\dfrac{3}{20}\right)^2+\dfrac{5573}{200}=0\)
Vì \(3\left(x-2\right)^2\ge0\)
\(6\left(y-\dfrac{3}{20}\right)^2\ge0\)
\(\dfrac{5573}{200}>0\)
\(\Rightarrow3\left(x-2\right)^2+6\left(y-\dfrac{3}{20}\right)^2+\dfrac{5573}{200}>0\)
Vậy biểu thức trên không có giá trị x,y thỏa mãn
Đúng 0
Bình luận (1)
Tìm x , y thỏa mãn :
a , \(3x^2+6y^2-12x-20y+40=0\)
b, \(3x^2+y^2+10x+2xy+26=0\)
Chứng minh rằng không có giá trị nào của x,y,z thỏa mãn đẳng thức sau :
\(x^2+4y^2+z^2-2x+8y-6z+15=0\)
\(x^2+4y^2+z^2-2x+8y-6z+15=0\)
\(\Leftrightarrow\left(x^2-2x+1\right)+\left(4y^2+8y+4\right)+\left(z^2-6z+9\right)+1=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2+1=0\)
Mà ta có
\(\hept{\begin{cases}\left(x-1\right)^2\ge0\\\left(2y+2\right)^2\ge0\\\left(z-3\right)^2\ge0\end{cases}}\)
\(\Rightarrow\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2+1>0\)
Vậy không tồn tại x, y, z thỏa mãn đẳng thức trên
Đúng 0
Bình luận (0)